
1. Giải bất phương trình \(\dfrac{1}{x} + \dfrac{x}{{x + 1}} < 1\) .
2. Giải và biện luận phương trình \(x + 4{m^2} \le 2mx + 1\) .

1. Ta có: \(\dfrac{1}{x} + \dfrac{x}{{x + 1}} < 1\)
\(\Leftrightarrow \dfrac{1}{x} + \dfrac{x}{{x + 1}} – 1 < 0\)
\( \Leftrightarrow \dfrac{{\left( {x + 1} \right) + {x^2} – x\left( {x + 1} \right)}}{{x\left( {x + 1} \right)}} < 0\)
\( \Leftrightarrow \dfrac{1}{{x\left( {x + 1} \right)}} < 0\)
Bảng xét dấu
Advertisements (Quảng cáo)
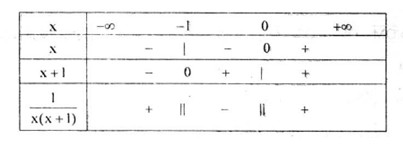
Bất phương trình có tập nghiệm \(S = \left( { – 1;0} \right)\) .
2. Ta có
\(x + 4{m^2} \le 2mx + 1\)
\(\Leftrightarrow 2mx – x \ge 4{m^2} – 1\)
Advertisements (Quảng cáo)
\( \Leftrightarrow \left( {2m – 1} \right)x \ge \left( {2m – 1} \right)\left( {2m + 1} \right)\)
Xét các trường hợp
+) \(2m – 1 = 0 \Leftrightarrow m = \dfrac{1}{2}\) : Bất phương trình trở thành \(0x \ge 0\) . Bất phương trình nghiệm đúng với mọi \(x \in \mathbb{R}\) .
+) \(2m – 1 > 0 \Leftrightarrow m > \dfrac{1}{2}\) : Bất phương trình có nghiệm x > 2m + 1.
+) \(2m – 1 < 0 \Leftrightarrow m < \dfrac{1}{2}\) : Bất phương trình có nghiệm x < 2m + 1.
Kết luận: \(m = \dfrac{1}{2}:S = \mathbb{R}\) .
\(m > \dfrac{1}{2}:S = \left( {2m + 1; + \infty } \right)\) .
\(m < \dfrac{1}{2}:S = \left( { – \infty 2m + 1} \right)\) .

