Bài 9: Cho đường tròn \((C):\,\,{x^2} + {y^2} = 4\) và điểm A(-2, 3)
a) Viết phương trình của các tiếp tuyến của (C) kể từ A.
b) Tính các khoảng cách từ A đến tiếp điểm của hai tiếp tuyến nói ở câu a) và khoảng cách giữa hai tiếp điểm đó.
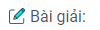
Đường tròn (C) có tâm O(0 ; 0), bán kính R=2.
a) Đường thẳng Δ qua A có dạng
\(\eqalign{
& a(x + 2) + b(y – 3) = 0 \cr
& \Leftrightarrow \,ax + by + 2a – 3b = 0 \cr} \)
Δ là tiếp tuyến của (C)
\(\eqalign{
& \Leftrightarrow \,\,d(O\,;\,\Delta ) = R\,\,\, \Leftrightarrow \,\,\,{{|2a – 3b|} \over {\sqrt {{a^2} + {b^2}} }} = 2 \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow \,\,{(2a – 3b)^2} = 4({a^2} + {b^2}) \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow \,\,5{b^2} – 12ab = 0 \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow \,\,b(5b – 12a) = 0\cr&\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\Leftrightarrow \,\,\,\left[ \matrix{
b = 0 \hfill \cr
12a = 5b \hfill \cr} \right. \cr} \)
Với b = 0, chọn a = 1 ta có tiếp tuyến \({\Delta _1}\,\,:\,\,x + 2 = 0\)
Với \(12a=5b\), chọn \(a=5, b=12\) ta có tiếp tuyến \({\Delta _2}:\,\,5x + 12y – 26 = 0\)
b) Gọi T, T’ là tiếp điểm của \({\Delta _1}\,,\,{\Delta _2}\) với (C) . Ta có
\(AT = AT’ = \sqrt {A{O^2} – {R^2}} = \sqrt {13 – 4} = 3\)
Advertisements (Quảng cáo)
Gọi H là giao điểm của TT’ và AO, TH là đường cao của tam giác vuông ATO, ta có
\(\eqalign{
& {1 \over {T{H^2}}} = {1 \over {A{T^2}}} + {1 \over {T{O^2}}} = {1 \over 9} + {1 \over 4} = {{13} \over {36}} \cr
& \Rightarrow \,\,TH = {6 \over {\sqrt {13} }}\,\, \Rightarrow \,\,\,TT’ = 2TH = {{12} \over {\sqrt {13} }} \cr} \
Bài 10: Cho \((E):{{{x^2}} \over 5} + {{{y^2}} \over 4} = 1\) và hypebol \((H):{{{x^2}} \over 5} – {{{y^2}} \over 4} = 1.\)
a) Tìm tọa độ các tiêu điểm của (E) và (H).
b) Vẽ phác elip (E) và hypebol (H) trong cùng một hệ trục tọa độ.
c) Tìm tọa độ các giao điểm của (E) và (H).
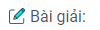
a) Với \((E):{{{x^2}} \over 5} + {{{y^2}} \over 4} = 1\) ta có \(a = \sqrt 5 \,,\,\,b = 2\,\,\, \Rightarrow \,c = \sqrt {{a^2} – {b^2}} = 1\)
Advertisements (Quảng cáo)
Tọa độ các tiêu điểm của (E) là \({F_1}( – 1\,;\,0)\,,\,\,{F_2}(1\,;\,0)\)
Với (H) : \({{{x^2}} \over 5} – {{{y^2}} \over 4} = 1\) , ta có \(a = \sqrt 5 \,,\,b = 2\,,\,\,c = \sqrt {{a^2} + {b^2}} = 3\)
Tọa độ các tiêu điểm của (H) là \({F_1}( – 3\,;\,0)\,,\,\,{F_2}(3\,;\,0)\)
b) Vẽ (E) và (H).
c) Tọa độ giao điểm của (E) và (H) là nghiệm của hệ phương trình
\(\left\{ \matrix{
{{{x^2}} \over 5} + {{{y^2}} \over 4} = 1 \hfill \cr
{{{x^2}} \over 5} – {{{y^2}} \over 4} = 1 \hfill \cr} \right.\,\,\,\, \Leftrightarrow \,\,\,\left\{ \matrix{
{x^2} = 5 \hfill \cr
{y^2} = 0 \hfill \cr} \right.\,\,\,\, \Leftrightarrow \,\,\,\left\{ \matrix{
x = \pm \sqrt 5 \hfill \cr
y = 0 \hfill \cr} \right.\)
Vậy tọa đô giao điểm của (E) và (H) là \(\left( {\sqrt 5 \,;\,0} \right)\) và \(\left( -{\sqrt 5 \,;\,0} \right)\) .
Bài 11: Cho đường thẳng \(\Delta :2x – y – m = 0\) và elip \((E):{{{x^2}} \over 5} + {{{y^2}} \over 4} = 1.\)
a) Với giá trị nào của m thì Δ cắt (E) tại hai điểm phân biệt?
b) Với giá trị nào của m thì Δ cắt (E) tại một điểm duy nhất?
Giải
Tọa độ giao điểm của Δ và (E) là nghiệm của hệ
\(\left\{ \matrix{
2x – y – m = 0 \hfill \cr
{{{x^2}} \over 5} + {{{y^2}} \over 4} = 1 \hfill \cr} \right.\Leftrightarrow \left\{ \matrix{
y = 2x – m\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1) \hfill \cr
{{{x^2}} \over 5} + {{{{(2x – m)}^2}} \over 4} = 1\,\,\,\,\,\,\,\,\,\,(2) \hfill \cr} \right.\)
Ta có (2) \( \Leftrightarrow \,\,4{x^2} + 5(4{x^2} – 4mx + {m^2}) = 20\)
\( \Leftrightarrow \,\,24{x^2} – 20mx + 5{m^2} – 20 = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(*)\)
a) Δ cắt (E) tại hai điểm phân biệt
⇔ (*) có hai nghiệm phân biệt
\(\eqalign{
& \Leftrightarrow \,\Delta ‘ = 100{m^2} – 24(5{m^2} – 20) > 0 \cr
& \Leftrightarrow \,\, – 20{m^2} + 480 > 0 \cr
& \Leftrightarrow \,\,|m| < 2\sqrt 6 \cr
& \Leftrightarrow \,\, – 2\sqrt 6 < m < 2\sqrt 6 \cr} \)
b) Δ cắt (E) tại một điểm duy nhất \( \Leftrightarrow \,\,m = \pm 2\sqrt 6 \)

