Bài 33: Cho elip \((E):{{{x^2}} \over 9} + {{{y^2}} \over 1} = 1.\)
a) Tính độ dài dây cung của (E) đi qua một tiêu điểm và vuông góc với trục tiêu (đoạn thẳng nối hai điểm của elip gọi là dây cung của elip, trục chứa các tiêu điểm gọi là trục tiêu của elip).
b) Tìm trên (E) điểm M sao cho \(M{F_1} = 2M{F_2}\) , trong đó \({F_1},{F_2}\) lần lượt là các tiêu điểm của (E) nằm bên trái và bên phải trục tung.
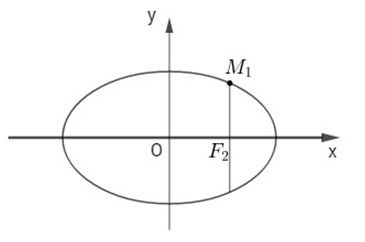
a) Ta có: \(a = 3;b = 1;c = \sqrt {{a^2} – {b^2}} = 2\sqrt 2 .\)
\({F_1}\left( { – 2\sqrt 2 ;0} \right);\,{F_2}\left( {2\sqrt 2 ;0} \right)\)
Gọi M là điểm trên (E) có hoành độ \(x = 2\sqrt 2 \)
Thay \(x = 2\sqrt 2 \) vào phương trình (E) ta được:
\({8 \over 9} + {{{y^2}} \over 1} = 1 \Leftrightarrow {y^2} = {1 \over 9} \Leftrightarrow y = \pm {1 \over 3}.\)
Vậy \({M_1}\left( {2\sqrt 2 ;{1 \over 3}} \right);{M_2}\left( {2\sqrt 2 ; – {1 \over 3}} \right)\) và độ dài dây cung cần tìm là \({M_1}{M_2} = {2 \over 3}\)
Advertisements (Quảng cáo)
b) Ta có:
\(\eqalign{
& M{F_1} = a + {c \over a}x = 3 + {{2\sqrt 2 } \over 3}x \cr
& M{F_2} = a – {c \over a}x = 3 – {{2\sqrt 2 } \over 3}x \cr
& M{F_1} = 2M{F_2} \Leftrightarrow 3 + {{2\sqrt 2 } \over 3}x = 6 – {{4\sqrt 2 } \over 3}x \cr&\Leftrightarrow 2\sqrt 2 x = 3 \Leftrightarrow x = {{3\sqrt 2 } \over 4}. \cr} \)
Thay \(x = {{3\sqrt 2 } \over 4}\) vào phương trình elip ta được:
\({2 \over {16}} + {y^2} = 1 \Leftrightarrow {y^2} = {7 \over 8} \Leftrightarrow y = \pm {{\sqrt {14} } \over 4}.\)
Vậy \({M_1}\left( {{{3\sqrt 2 } \over 4};{{\sqrt {14} } \over 4}} \right);{M_2}\left( {{{3\sqrt 2 } \over 4}; – {{\sqrt {14} } \over 4}} \right).\)
Bài 34: Vệ tinh nhân tạo đầu tiên được Liên Xô (cũ) phóng từ Trái đất năm 1957. Quỹ đạo của vệ tinh đó là một đường elip nhận tâm Trái Đất là một tiêu điểm. Nguowiff ta đo được vệ tinh cách bề mặt Trái Đất gần nhất là 583 dặm và xa nhất là 1342 dặm (1 dặm \( \approx 1,609km\)). Tìm tâm sai của quỹ đạo đó biết bán kính của Trái Đất xấp xỉ 4000 dặm.
Advertisements (Quảng cáo)
Giả sử tâm trái đất là: \({F_1}\left( { – c;0} \right)\)
\(M{F_1}\) có giá trị nhỏ nhất là: \(a – c\) và có giá trị lớn nhất là \(a + c \). Do đó
\(\eqalign{
& a + c = 1342 + 4000 = 5342 \cr
& a – c = 583 + 4000 = 4583 \cr} \)
Từ đó suy ra: \(2a = 9925;2c = 759.\)
Do đó: \(e = {c \over a} = {{759} \over {9925}} \approx 0,07647.\)
Bài 35: Trong mặt phẳng tọa độ Oxy, cho điểm A chạy trên trục Ox, điểm B chạy trên trục Oy nhưng độ dài đoạn AB bằng a không đổi. Tìm tập hợp các điểm M thuộc đoạn AB sao cho \(MB = 2MA.\)
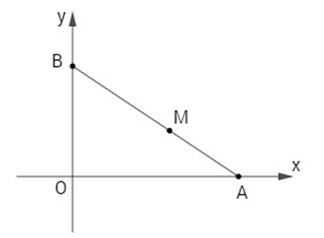
Giả sử: \(A\left( {{x_0};0} \right);B\left( {0;{y_0}} \right)\)
\(AB = a \Leftrightarrow \sqrt {x_0^2 + y_0^2} = a \Leftrightarrow x_0^2 + y_0^2 = {a^2}\)
M thuộc đoạn AB và \(MB = 2MA\) nên \(\overrightarrow {AM} = {1 \over 3}\overrightarrow {AB} \)
Giả sử: M(x, y) , khi đó: \(\overrightarrow {AM} = \left( {x – {x_0};y} \right),\overrightarrow {AB} = \left( { – {x_0};{y_0}} \right);\)
\(3\overrightarrow {AM} = \overrightarrow {AB} .\)
\(\eqalign{
& \Leftrightarrow \left\{ \matrix{
3\left( {x – {x_0}} \right) = – {x_0} \hfill \cr
3y = {y_0} \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
{x_0} = {3 \over 2}x \hfill \cr
{y_0} = 3y \hfill \cr} \right. \cr
& x_0^2 + y_0^2 = {a^2} \Leftrightarrow {9 \over 4}{x^2} + 9{y^2} = {a^2} \cr&\Leftrightarrow {{{x^2}} \over {{{\left( {{{2a} \over 3}} \right)}^2}}} + {{{y^2}} \over {{{\left( {{a \over 3}} \right)}^2}}} = 1 \cr} \)
Vậy tập hợp điểm M là elip có phương trình là:
\({{{x^2}} \over {{{\left( {{{2a} \over 3}} \right)}^2}}} + {{{y^2}} \over {{{\left( {{a \over 3}} \right)}^2}}} = 1.\)

