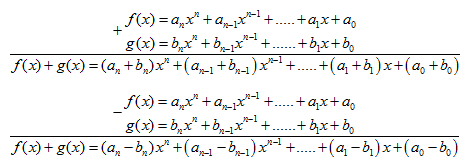Câu 38: Tính f(x) + g(x) với:
\(f\left( x \right) = {x^5} – 3{{\rm{x}}^2} + {x^3} – {x^2} – 2{\rm{x}} + 5\)
\(g\left( x \right) = {x^2} – 3{\rm{x}} + 1 + {x^2} – {x^4} + {x^5}\)
Thu gọn rồi sắp xếp đa thức theo lũy thừa giảm của biến :
\(\eqalign{
& f\left( x \right) = {x^5} – 3{{\rm{x}}^2} + {x^3} – {x^2} – 2{\rm{x}} + 5 \cr
& \Leftrightarrow f(x) = {x^5} + {x^3} – {x^2} – 2{\rm{x}} + 5 \cr} \)
\(\eqalign{
& g\left( x \right) = {x^2} – 3{\rm{x}} + 1 + {x^2} – {x^4} + {x^5} \cr
& \Leftrightarrow g(x) = {x^5} – {x^4} + 2{x^2} – 3{\rm{x}} + 1 \cr} \)

Câu 39: Tính f(x) – g(x) với :
\(f(x) = {x^7} – 3{{\rm{x}}^2} – {x^5} + {x^4} – {x^2} + 2{\rm{x}} – 7\)
\(g(x) = x – 2{{\rm{x}}^2} + {x^4} – {x^5} – {x^7} – 4{{\rm{x}}^2} – 1\)
Advertisements (Quảng cáo)
Thu gọn rồi sắp xếp đa thức theo lũy thừa giảm của biến:
\(\eqalign{
& f(x) = {x^7} – 3{{\rm{x}}^2} – {x^5} + {x^4} – {x^2} + 2{\rm{x}} – 7 \cr
& \Leftrightarrow f(x) = {x^7} – {x^5} + {x^4} – 4{x^2} + 2{\rm{x}} – 7 \cr} \)
\(\eqalign{
& g(x) = x – 2{{\rm{x}}^2} + {x^4} – {x^5} – {x^7} – 4{{\rm{x}}^2} – 1 \cr
& \Leftrightarrow g(x) = – {x^7} – {x^5} + {x^4} – 6{{\rm{x}}^2} + x – 1 \cr} \)
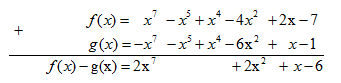
Câu 40: Cho các đa thức:
\(f(x) = {x^4} – 3{{\rm{x}}^2} + x – 1\)
\(g(x) = {x^4} – {x^3} + {x^2} + 5\)
Advertisements (Quảng cáo)
Tìm đa thức h(x) sao cho:
a) f(x) + h(x) = g(x)
b) f(x) – h(x) = g(x)
a) f (x) + h (x) = g (x)
\( \Rightarrow h(x) = g(x) – f(x) \)
\(h(x)= \left( {{x^4} – {x^3} + {x^2} + 5} \right) – ({x^4} – 3{{\rm{x}}^2} + x – 1)\)
\(\eqalign{
& h(x) = {x^4} – {x^3} + {x^2} + 5 – {x^4} + 3{{\rm{x}}^2} – x + 1 \cr
& h(x) = – {x^3} + 4{{\rm{x}}^2} – x + 6 \cr} \)
b) f (x) – h (x) = g (x)
\(\eqalign{
& \Rightarrow h(x) = f(x) – g(x) \cr
& \Leftrightarrow h(x) = ({x^4} – 3{{\rm{x}}^2} + x – 1) – ({x^4} – {x^3} + {x^2} + 5) \cr} \)
\(\eqalign{
& \Leftrightarrow h(x) = {x^4} – 3{{\rm{x}}^2} + x – 1 – {x^4} + {x^3} – {x^2} – 5 \cr
& \Leftrightarrow h(x) = {x^3} – 4{x^2} + x – 6 \cr} \)
Câu 41: Cho đa thức:
\(f(x) = {a_n}{x^n} + {a_{n – 1}}{x^{n – 1}} + … + {a_1}x + {a_0}\)
\(g(x) = {b_n}{x^n} + {b_{n – 1}}{x^{n – 1}} + …. + {b_1}x + {b_0}\)
a) Tính f (x) + g (x)
b) Tính f (x) – g (x)