Câu 15: Tam giác ABC có số đo các góc A, B, C tỉ lệ với 3; 5; 7. Tính số đo các góc của tam giác ABC (biết rằng tổng số đo ba góc trong một tam giác 180°)
Gọi a, b, c (độ) là số đo của 3 góc A, B, C.
Vì số đo các góc tỉ lệ với 3; 5; 7 nên ta có:
\(\eqalign{
& {a \over 3} = {b \over 5} = {c \over 7} = {{a + b + c} \over {3 + 5 + 7}} = {{180} \over {15}} = 12 \cr
& {a \over 3} = 12 \Rightarrow a = 3.12 = 36 \cr
& {b \over 5} = 12 \Rightarrow b = 5.12 = 60 \cr
& {c \over 7} = 12 \Rightarrow c = 7.12 = 84 \cr} \)
Vậy số đo các góc A, B, C theo thứ tự là 36°, 60°, 84°.
Câu 16: Gọi x, y, z theo thứ tự là số vòng quay của kim giờ, kim phút, kim giây trong cùng một thời gian.
a) Điền số thích hợp vào các ô trống trong hai bảng sau:
|
x |
1 |
2 |
3 |
4 |
|
y |
|
|
|
|
|
y |
1 |
6 |
12 |
18 |
|
z |
|
|
|
|
b) Viết công thức biểu diễn y theo x và z theo y
c) Số vòng quay x của kim giờ và số vòng quay z của kim giây có tỉ lệ thuận với nhau không? Nếu có, hãy tìm hệ số tỉ lệ của z đối với x.
Advertisements (Quảng cáo)
d) Khi kim giờ quay được 5 vòng thì kim giây quay được bao nhiêu vòng?
a)
|
x |
1 |
2 |
3 |
4 |
|
y |
12 |
24 |
36 |
48 |
|
y |
1 |
6 |
12 |
18 |
|
z |
60 |
360 |
720 |
1080 |
b) y = 12x; z = 60y
c) Ta có: z = 60. (12x) = 720x
Số vòng quay của kim giờ x và số vòng quay của kim giây z là hai đại lượng tỉ lệ thuận với nhau.
Advertisements (Quảng cáo)
Hệ số tỉ lệ của z đối với x là 720
d) Thay x = 5 vào biểu thức z = 720x ta có:
z = 720. 5 = 3600(vòng)
Câu 17: Đố vui: Một kết quả bất ngờ. Biết rằng bán kính Trái Đất \({R_{T{\rm{D}}}} \approx 6370km\) (hình dưới). Giả sử một chiếc vệ tinh bay vòng quanh Trái Đất và cách mặt đất 100km.
a) Em hãy dự đoán xem quãng đường vệ tinh một vòng dài hơn chu vi Trái Đất khoảng bao nhiêu ki-lô-mét: trên 1000km hay dưới 1000km?
b) Em hãy tính cụ thể và cho biết kết quả.
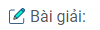
a) Vì vệ tinh cách mặt đất là 100km nên chu vi vệ tinh quay vòng hơn chu vi trái đất một khoảng 2.3,14.100 nên nhỏ hơn 1000km
b) Gọi bán kính của Trái Đất \({{\rm{R}}_{T{\rm{D}}}}\), bán kính quỹ đạo vệ tinh \({{\rm{R}}_{VT}}\)
Chu vi trái đất \({\rm{2}}\pi {{\rm{R}}_{T{\rm{D}}}}\), chu vi quỹ đạo vệ tinh \({\rm{2}}\pi {{\rm{R}}_{VT}}\)
Vì chu vi của đường tròn tỉ lệ thuận với bán kính nên ta có:
\(\eqalign{
& {{{\rm{2}}\pi {{\rm{R}}_{VT}}} \over {{\rm{2}}\pi {{\rm{R}}_{T{\rm{D}}}}}} = {{{{\rm{R}}_{VT}}} \over {{{\rm{R}}_{T{\rm{D}}}}}} \cr
& \Rightarrow {{{\rm{2}}\pi {{\rm{R}}_{VT}} – {\rm{2}}\pi {{\rm{R}}_{T{\rm{D}}}}} \over {{\rm{2}}\pi {{\rm{R}}_{T{\rm{D}}}}}} = {{{{\rm{R}}_{VT}} – {{\rm{R}}_{T{\rm{D}}}}} \over {{{\rm{R}}_{T{\rm{D}}}}}} \cr
& \Rightarrow {\rm{2}}\pi {{\rm{R}}_{VT}} – {\rm{2}}\pi {{\rm{R}}_{T{\rm{D}}}} = {{{\rm{2}}\pi {{\rm{R}}_{T{\rm{D}}}}({{\rm{R}}_{VT}} – {{\rm{R}}_{T{\rm{D}}}})} \over {{{\rm{R}}_{T{\rm{D}}}}}} \cr
& \Rightarrow {\rm{2}}\pi {{\rm{R}}_{VT}} – {\rm{2}}\pi {{\rm{R}}_{T{\rm{D}}}} = 2\pi .100 \approx 628(km) \cr} \)
Quãng đường vệ tinh bay dài hơn chu vi trái đất khoảng 628km.

