Bài 34: Giải hệ phương trình sau ( có thể dùng máy tính bỏ túi để kiểm tra kết quả – Xem bài đọc thêm
\(\left\{ \matrix{
x + y + z = 11 \hfill \cr
2x – y + z = 5 \hfill \cr
3x + 2y + z = 24 \hfill \cr} \right.\)
Lấy (1) trừ (2), ta được: -x + 2y = 6
Lấy (2) trừ (3), ta được: -x – 3y = -19
Ta có hệ:
\(\left\{ \matrix{
x – 2y = – 6 \hfill \cr
x + 3y = 19 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = 4 \hfill \cr
y = 5 \hfill \cr} \right.\)
Thay x = 4, y = 5 vào (1), ta được z = 2
Vậy hệ có nghiệm (4, 5, 2)
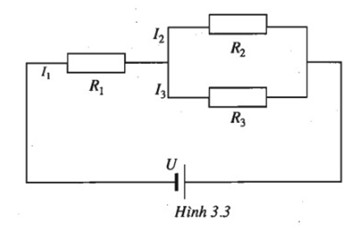
Bài 35: Cho một mạch điện kín. Biết R1 = 0,250, R2 = 0,360, R3 = 0,450 và U = 0,6V. Gọi I1 là cường độ dòng điện của mạch chính, I2 và I3 là cường độ dòng diện của mạch rẽ. Tính I1, I2, I3 (chính xác đến phần trăm).
Advertisements (Quảng cáo)
Ta có hệ phương trình ẩn I1; I2; I3
\(\left\{ \matrix{
{I_1} = {I_2} + {I_3} \hfill \cr
{R_1}{I_1} + {R_2}{I_2} = U \hfill \cr
{R_2}{I_2} = {R_3}{I_3} \hfill \cr} \right. \)
\(\Leftrightarrow \left\{ \matrix{
{I_1} – {I_2} – {I_3} = 0 \hfill \cr
0,25{I_1} + 0,36{I_2} = 0,6 \hfill \cr
0,36{I_2} – 0,45{I_3} = 0 \hfill \cr} \right. \)
\(\Leftrightarrow \left\{ \matrix{
{I_1} \approx 1,33A \hfill \cr
{I_2} \approx 0,74A \hfill \cr
{I_3} \approx 0,59A \hfill \cr} \right.\)
Bài 36: Cho một hệ hai phương trình bậc nhất hai ẩn. Biết rằng phương trình thứ hai trong hệ vô nghiệm. Hãy chọn kết luận đúng trong các khẳng định sau:
(A) Hệ đã cho nghiệm đúng với mọi giá trị của ẩn;
(B) Hệ đã cho vô nghiệm;
(C) Tập nghiệm của hệ đã cho trùng với tập nghiệm của phương trình thứ nhất;
Advertisements (Quảng cáo)
(D) Không có kết luận gì.
Hệ đã cho vô nghiệm
Chọn (B)
Bài 37: Tính nghiệm gần đúng của hệ phương trình sau (chính xác đến hàng phần trăm):
a)
\(\left\{ \matrix{
\sqrt 3 x – y = 1 \hfill \cr
5x + \sqrt 2 y = \sqrt 3 \hfill \cr} \right.\)
b)
\(\left\{ \matrix{
4x + (\sqrt 3 – 1)y = 1 \hfill \cr
(\sqrt 3 + 1)x + 3y = 5 \hfill \cr} \right.\)
Đáp án
a) Ta có:
\(\eqalign{
& D = \,\left|\matrix{
{\sqrt 3 } & -1 \cr
5 & {\sqrt 2 } \cr}\right|\, = \sqrt 6 + 5 \cr & {D_x} = \,\left|\matrix{1 & { – 1} \cr {\sqrt 3 } & {\sqrt 2 } \cr} \right|\, = \sqrt 2 + \sqrt 3 \cr & {D_y} = \,\left|\matrix{{\sqrt 3 } & 1 \cr 5 & {\sqrt 3 } \cr}\right |\, = – 2 \cr} \)
Hệ phương trịnh có nghiệm duy nhất (x, y) với:
\(\left\{ \matrix{
x = {{{D_x}} \over D} = {{\sqrt 2 + \sqrt 3 } \over {\sqrt 6 + 5}} \approx 0,42 \hfill \cr
y = {{{D_y}} \over D} = {{ – 2} \over {\sqrt 6 + 5}} \approx – 0,27 \hfill \cr} \right.\)
b) Ta có:
\(\eqalign{
& D = \left|\matrix{
4 & {\sqrt 3 – 1} \cr
{\sqrt 3 + 1} & 3 \cr} \right|\, = 12 – (3 – 1) = 10 \cr & {D_x} = \,\left|\matrix{1 & {\sqrt 3 – 1} \cr 5 & 3 \cr} \right|\, = 3 – 5(\sqrt 3 – 1) = 8 – 5\sqrt 3 \cr & {D_y} = \,\left|\matrix{4 & 1 \cr {\sqrt 3 + 1} & 5 \cr} \right |\, = 20 – (\sqrt 3 + 1) = 19 – \sqrt 3 \cr} \)
Hệ có nghiệm duy nhất là:
\(\left\{ \matrix{
x = {{8 – 5\sqrt 3 } \over {10}} \approx – 0,07 \hfill \cr
y = {{19 – \sqrt 3 } \over {10}} \approx 1,73 \hfill \cr} \right.\)

