Bài 50: Phương trình ax + b = 0 có thể có nghiệm trong những trường hợp nào?
Nếu \(a ≠ 0\) thì phương trình có nghiệm duy nhất \(x = – {b \over a}\)
Nếu \(a = 0, b = 0\) thì phương trình có vô số nghiệm,
Vậy phương trình có nghiệm khi \(a ≠ 0\) hoặc \(a = b = 0\)
Bài 51: Giả sử ba phương trình f(x).g(x) = 0, f(x) = 0 và g(x) = 0 (với cùng tập xác định) có các tập nghiệm lần lượt là T, T1 và T2. Hãy chọn kết luận đúng trong hai kết luận sau:
a) S = S1 ∩ S2;
b) S = S1 ∪ S2.
Ta có:
\(f(x).g(x) = 0 \Leftrightarrow \left[ \matrix{
f(x) = 0 \hfill \cr
g(x) = 0 \hfill \cr} \right.\)
Advertisements (Quảng cáo)
Chọn b) S = S1 ∪ S2
Bài 52: Hệ phương trình dạng
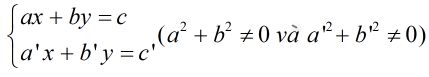
có thể có nghiệm trong trường hợp nào?
Áp dụng: Tìm a để hệ có phương trình
\(\left\{ \matrix{
ax + y = {a^2} \hfill \cr
x + ay = 1 \hfill \cr} \right.\) có nghiệm?
Advertisements (Quảng cáo)
Hệ đã cho có nghiệm khi D ≠ 0 hoặc D = Dx = Dy = 0
Áp dụng:
Ta có:
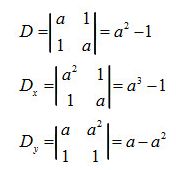
+ Nếu \(a ≠ ± 1\) hệ có nghiệm duy nhất
+ Nếu \(a = 1\) thì hệ có vô số nghiệm
+ Nếu \(a = -1\) thì hệ vô nghiệm (Do Dx = -2 ≠ 0)
Vậy hệ có nghiệm \(⇔ a ≠ -1\)
Bài 53: Biết rằng phương trình ax2 + bx + c = 0 có một nghiệm kép xo. Hãy chọn mệnh đề đúng trong các mệnh đề sau:
(A) Tam thức bậc hai ax2 + bx + c có thể viết dưới dạng bình phương của một nhị thức bậc nhất;
(B) Parabol y = ax2 + bx + c có đỉnh thuộc trục hoành;
(C) Phương trình cx2 + bx + a = 0 cũng có một nghiệm kép là \({1 \over {{x_0}}}\)
Chọn (B). (P) có đỉnh thuộc trục hoành
Chú ý (A) chỉ đúng nếu a > 0
(C) chỉ đúng nếu c ≠ 0

