Bài 5: Một hình bình hành có hai cạnh nằm trên hai đường thẳng x + 3y – 6 = 0 và 2x – 5y – 1 = 0. Biết hình bình hành đó có tâm đối xứng là I(3, 5). Hãy viết phương trình hai cạnh còn lại của hình bình hành đó.
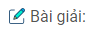
Giả sử hình bình hành ABCD có tâm I
\(\eqalign{
& AB:\,\,x + 3y – 6 = 0 \cr
& AD:\,\,2x – 5y – 1 = 0 \cr} \)
Tọa độ của A là nghiệm của hệ
\(\left\{ \matrix{
x + 3y – 6 = 0 \hfill \cr
2x – 5y – 1 = 0 \hfill \cr} \right.\,\,\, \Leftrightarrow \,\,\,\left\{ \matrix{
x = 3\, \hfill \cr
y = 1 \hfill \cr} \right.\)
Vậy \(A(3 ; 1)\).
I là trung điểm của AC nên
\(\left\{ \matrix{
{x_I} = {1 \over 2}({x_A} + {x_C}) \hfill \cr
{y_I} = {1 \over 2}({y_A} + {y_C}) \hfill \cr} \right.\,\,\,\, \Leftrightarrow \,\,\left\{ \matrix{
{x_C} = 2{x_I} – {x_A} = 3 \hfill \cr
{y_C} = 2{y_I} – {y_A} = 9 \hfill \cr} \right.\)
Vậy \(C(3 ; 9)\).
BC là đường thẳng qua C và song song với AD nên BC có phương trình:
\(2(x – 3) – 5(y – 9) = 0\,\, \Leftrightarrow \,\,2x – 5y + 39 = 0\)
CD là đường thẳng qua C và song song với AB nên CD có phương trình:
\(1(x – 3) + 3(y – 9) = 0\,\, \Leftrightarrow \,\,x + 3y – 30 = 0\)
Vậy hai cạnh còn lại của hình bình hành là
Advertisements (Quảng cáo)
\(2x – 5y + 39 = 0\) và \(x + 3y – 30 = 0\)
Bài 6: Cho phương trình
\({x^2} + {y^2} + mx – 2(m + 1)y + 1 = 0.\,\,\,\,\,(1)\)
a) Với giá trị nào của m thì (1) là phương trình đường tròn?
b) Tìm tập hợp tâm của các đường tròn nói ở câu a).
Giải
a) Ta có: \(2a = m\,,\,2b = – 2(m + 1)\,,\,\,c = 1\)
\(\Rightarrow \,\,a = {m \over 2}\,,\,\,b = – (m + 1)\,,\,\,c = 1\)
(1) là đường tròn \( \Leftrightarrow \,\,{a^2} + {b^2} – c > 0\,\, \Leftrightarrow \,\,{{{m^2}} \over 4} + {(m + 1)^2} – 1 > 0\)
\( \Leftrightarrow \,\,{5 \over 4}{m^2} + 2m > 0\,\,\, \Leftrightarrow \,\,\,\left[ \matrix{
m < – {8 \over 5}\, \hfill \cr
m > 0 \hfill \cr} \right.\,\,\)
Advertisements (Quảng cáo)
b) Với điều kiện \(m < – {8 \over 5}\) hoặc m > 0 thì (1) là phương trình đường tròn có tâm \(I\left( { – {m \over 2}\,;\,m + 1} \right)\) .
Ta có tọa độ của I
\(\left\{ \matrix{
x = – {m \over 2} \hfill \cr
y = m + 1 \hfill \cr} \right.\)
Khử m từ hoành độ và tung độ của I ta được \(2x + y – 1 = 0\) vì \(m < – {8 \over 5}\) hoặc m > 0 nên \(x = – {m \over 2} > {4 \over 5}\) hoặc \(x < 0\) .
Vậy tập hợp tâm I của đường tròn là
\(\left\{ \matrix{
2x + y – 1 = 0 \hfill \cr
\left[ \matrix{
x < 0 \hfill \cr
x > {4 \over 5} \hfill \cr} \right.\, \hfill \cr} \right.\)
Bài 7: a) Biết đường tròn (C) có phương trình \({x^2} + {y^2} + 2ax + 2by + c = 0.\) Chứng minh rằng phương tích của điểm \(M({x_0};{y_0})\) đối với đường tròn (C) bằng \(x_0^2 + y_0^2 + 2a{x_0} + 2b{y_0} + c.\)
b) Chứng minh rằng nếu hai đường tròn không đồng tâm thì tập hợp các điểm có cùng phương tích đối với hai đường tròn là một đường thẳng (gọi là trục đẳng phương của hai đường tròn).
a) Đường tròn (C) có tâm I(-a, -b) ,bán kính \(R = \sqrt {{a^2} + {b^2} – c} \)
Phương tích của điểm \(M({x_0};{y_0})\) đối với đường tròn (C) là
\(\eqalign{
& {\wp _{{M_{{/_{(C)}}}}}} = M{I^2} – {R^2} \cr&\,\,\,\,\,\,\,\,\,\,\,\,\,\,= {({x_o} + a)^2} + {({y_o} + b)^2} – ({a^2} + {b^2} – c) \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\, = x_o^2 + y_o^2 + 2a{x_o} + 2b{y_o} + c \cr} \)
b) Cho hai đường tròn không đồng tâm
\(\eqalign{
({C_1})\, & & :\,\,{x^2} + {y^2} + 2{a_1}x + 2{b_1}y + {c_1} \cr
({C_2})\, & & :\,\,{x^2} + {y^2} + 2{a_2}x + 2{b_2}y + {c_2} \cr} \)
Gọi \(M({x_0};{y_0})\) là điểm có cùng phương tích đối với \(({C_1})\) và \(({C_2})\) thì
\(\eqalign{
& \,\,\,\,\,\,\,x_o^2 + y_o^2 + 2{a_1}{x_o} + 2{b_1}{y_o} + {c_1} = x_o^2 + y_o^2 \cr&+ 2{a_2}{x_o} + 2{b_2}{y_o} + {c_2} \cr
& \Leftrightarrow \,\,2({a_1} – {a_2}){x_o} + 2({b_1} – {b_2}){y_o} + {c_1} – {c_2} = 0\,\,\,(1) \cr} \)
Vì \(({C_1})\) và \(({C_2})\) không đồng tâm nên \({a_1} – {a_2}\) và \({b_1} – {b_2}\) không đồng thời bằng 0 ( tức \({({a_1} – {a_2})^2} + {({b_1} – {b_2})^2} \ne 0\))
Do đó \(M({x_0};{y_0})\) nằm trên đường thẳng có phương trình:
\(\Delta \,\,:\,\,2({a_1} – {a_2})x + 2({b_1} – {b_2})y + {c_1} – {c_2} = 0\)
Vậy tập hợp điểm M là đường thẳng Δ .
Bài 8: Cho hai đường tròn có phương trình \({x^2} + {y^2} + 2{a_1}x + 2{b_1}y + {c_1} = 0\) và \({x^2} + {y^2} + 2{a_2}x + 2{b_2}y + {c_2} = 0.\) Giả sử chúng cắt nhau ở hai điểm M,N. Viết phương trình đường thẳng MN.
Hai đường tròn cắt nhau tại M, N thì trục đẳng phương của chùng chính là đường thẳng MN.
Áp dụng bài 7 thì MN có phương trình là
\(MN\,:\,\,2({a_1} – {a_2})x + 2({b_1} – {b_2})y + {c_1} – {c_2} = 0\)

