Bài 11: Cho tam giác đều \(ABC\) có cạnh bằng \(a\). Giá trị \(\left| {\overrightarrow {AB} – \overrightarrow {CA} } \right|\) bằng bao nhiêu ?
(A) \(2a\) ; (B) \(a\);
(C) \(a\sqrt 3 \); (D) \({{a\sqrt 3 } \over 2}\).
Hướng dấn trả lời
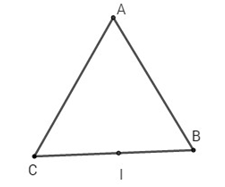
Gọi \(I\) là trung điểm \(BC\).
Ta có \(\overrightarrow {AB} – \overrightarrow {CA} = \overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AI} \).
\( \Rightarrow \,\,\left| {\overrightarrow {AB} – \overrightarrow {CA} } \right| = \left| {2\overrightarrow {AI} } \right| = 2.{{a\sqrt 3 } \over 2} = a\sqrt 3 .\)
Chọn (C).
Bài 12: Cho hai tam giác \(ABC\) và \(A’B’C’\) lần lượt có trọng tâm là \(G\) và \(G’\). Đẳng thức nào dưới đây là sai ?
(A) \(3\overrightarrow {G{G’}} = \overrightarrow {A{A’}} + \overrightarrow {B{B’}} + \overrightarrow {C{C’}} \);
Advertisements (Quảng cáo)
(B) \(3\overrightarrow {G{G’}} = \overrightarrow {A{B’}} + \overrightarrow {B{C’}} + \overrightarrow {C{A’}} \);
(C) \(3\overrightarrow {G{G’}} = \overrightarrow {A{C’}} + \overrightarrow {B{A’}} + \overrightarrow {C{B’}} \) ;
(D) \(3\overrightarrow {G{G’}} = \overrightarrow {{A’}A} + \overrightarrow {B{B’}} + \overrightarrow {C{C’}} \).

Chọn (D).
Bài 13: Cho điểm \(B\) nằm giữa hai điểm \(A\) và \(C\), với \(AB = 2a, AC = 6a\). Đẳng thức nào dưới đây đúng ?
Advertisements (Quảng cáo)
(A) \(\overrightarrow {BC} = \overrightarrow {AB} \) ;
(B) \(\overrightarrow {BC} = – 2\overrightarrow {AB} \) ;
(C) \(\overrightarrow {BC} = 4\overrightarrow {AB} \) ;
(D) \(\overrightarrow {BC} = – 2\overrightarrow {BA} \) .

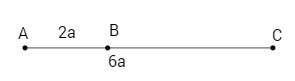
Ta có \(\overrightarrow {BC} = 2\overrightarrow {AB} = – 2\overrightarrow {BA} \).
Chọn (D).
Bài 14: Cho ba điểm phân biệt \(A, B, C\). Nếu \(\overrightarrow {AB} = – 3\overrightarrow {AC} \) thì đẳng thức nào dưới đây đúng ?
(A) \(\overrightarrow {BC} = 4\overrightarrow {AC} \);
(B) \(\overrightarrow {BC} = – 4\overrightarrow {AC} \);
(C) \(\overrightarrow {BC} = 2\overrightarrow {AC} \);
(D) \(\overrightarrow {BC} = – 2\overrightarrow {AC} \);

Ta có \(\overrightarrow {BC} = \overrightarrow {BA} + \overrightarrow {AC} = – \overrightarrow {AB} + \overrightarrow {AC} = 3\overrightarrow {AC} + \overrightarrow {AC} = 4\overrightarrow {AC} .\)
Chọn (A).

