Bài 1.48: Cho hình bình hành ABCD tâm O. Gọi M và N lần lượt là trung điểm của AD và BC. Dựa vào các điểm A, B, C, D, O, M, N đã cho, hãy:
a) Kể tên hai vec tơ cùng phương với \(\overrightarrow {AB} \), hai vec tơ cùng hướng với \(\overrightarrow {AB} \), hai vec tơ ngược hướng với \(\overrightarrow {AB} \) (các vec tơ kể ra này đều khác \(\overrightarrow 0 \))
b) Chỉ ra một vec tơ bằng vec tơ \(\overrightarrow {MO} \), một vec tơ \(\overrightarrow {OB} \)

(Xem h.162)
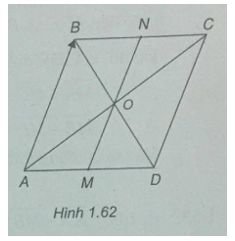
a) Hai vec tơ cùng phương với \(\overrightarrow {AB} \) là \(\overrightarrow {MO} ,\overrightarrow {CD} \);
Hai vec tơ cùng hướng với \(\overrightarrow {AB} \) là \(\overrightarrow {ON} ,\overrightarrow {DC} \);
Hai vec tơ ngược hướng với \(\overrightarrow {AB} \) là \(\overrightarrow {OM} ,\overrightarrow {NO} \);
b) Vec tơ \(\overrightarrow {MO} \) là \(\overrightarrow {ON} \)
Vec tơ \(\overrightarrow {OB} \) là \(\overrightarrow {DO} \)
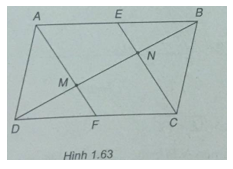
Bài 1.49: Cho hình bình hành ABCD. Gọi E và F lần lượt là trung điểm của hai cạnh AB và CD. Nối AF và CE, hai đường thẳng này cắt đường chéo BD lần lượt tại M và N. Chứng minh \(\overrightarrow {DM} = \overrightarrow {MN} = \overrightarrow {NB} \)
Advertisements (Quảng cáo)

(h.1.63)
AECF là hình bình hành => EN // AM
E là trung điểm của AB => N là trung điểm của BM, do đó MN = NB.
Tương tự, M là trung điểm của DN, do đó DM = MN.
Vậy \(\overrightarrow {DM} = \overrightarrow {MN} = \overrightarrow {NB} \)
Bài 1.50: Cho hai hình bình hành ABCD và ABEF với A, D, F không thẳng hàng. Dựng các vec tơ $\(\overrightarrow {EH} \) và \(\overrightarrow {FG} \) bằng vec tơ \(\overrightarrow {AD} \). Chứng minh tứ giác CDGH là hình bình hành.
Advertisements (Quảng cáo)

(h.1.64)
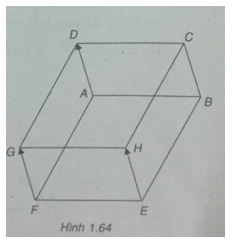
\(\overrightarrow {EH} = \overrightarrow {AD} ,\overrightarrow {FG} = \overrightarrow {AD} = > \overrightarrow {EH} = \overrightarrow {FG} \)
=>Tứ giác FEHG là hình bình hành
\( = > \overrightarrow {GH} = \overrightarrow {FE} \,(1)\)
Ta có: \(\overrightarrow {DC} = \overrightarrow {AB} ,\overrightarrow {AB} = \overrightarrow {FE} \)
\(\overrightarrow { = > DC} = \overrightarrow {FE} \,(2)\)
Từ (1) và (2) ta có \(\overrightarrow {GH} = \overrightarrow {DC} \)
Vậy tứ giác GHCD là hình bình hành.
Bài 1.51: Cho bốn điểm A, B, C, D. Tìm các vec tơ:
a) \(\overrightarrow u = \overrightarrow {AB} + \overrightarrow {DC} + \overrightarrow {BD} + \overrightarrow {CA} \)
b) \(\overrightarrow v = \overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {BC} + \overrightarrow {DA} \)

a)
\(\eqalign{
& \overrightarrow u = \overrightarrow {AB} + \overrightarrow {DC} + \overrightarrow {BD} + \overrightarrow {CA} \cr
& = (\overrightarrow {AB} + \overrightarrow {BD} ) + (\overrightarrow {DC} + \overrightarrow {CA} ) \cr
& = \overrightarrow {AD} + \overrightarrow {DA} = \overrightarrow {AA} = \overrightarrow 0 \cr} \)
b)
\(\eqalign{
& \overrightarrow v = \overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {BC} + \overrightarrow {DA} \cr
& = (\overrightarrow {DA} + \overrightarrow {AB} ) + (\overrightarrow {BC} + \overrightarrow {CD} ) \cr
& = \overrightarrow {DB} + \overrightarrow {BD} = \overrightarrow {DD} = \overrightarrow 0 \cr} \)

