Bài 1.44: Cho tam giác ABC có A( – 5;6), B( – 4; – 1), C(4;3). Tìm tọa độ trung điểm I của AC. Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành.

(h.1.58)
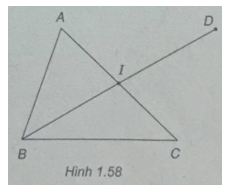
Gọi I là trung điểm của AC
\(\eqalign{
& {x_I} = {{ – 5 + 4} \over 2} = – {1 \over 2}, \cr
& {y_I} = {{6 + 3} \over 2} = {9 \over 2} \cr} \)
Tứ giác ABCD là hình bình hành I là trung điểm của BD.
Vậy
\(\eqalign{
& \left\{ \matrix{
{{{x_D} – 4} \over 2} = – {1 \over 2} \hfill \cr
{{{y_D} – 1} \over 2} = {9 \over 2} \hfill \cr} \right. = > \left\{ \matrix{
{x_D} – 4 = – 1 \hfill \cr
{y_D} – 1 = 9 \hfill \cr} \right. \cr
& = > \left\{ \matrix{
{x_D} = 3 \hfill \cr
{y_D} = 10 \hfill \cr} \right. \cr} \)
Vậy tọa độ đỉnh D là (3;10).
Bài 1.45: Cho tam giác ABC có A(- 3;6), B(9; -10), C( -5;4).
a) Tìm tọa độ của trọng tâm G của tam giác ABC
b) Tìm tọa độ điểm D sao cho tứ giác BGCD là hình bình hành

(h.1.59)
Advertisements (Quảng cáo)
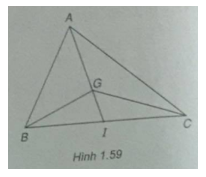
a) \(\left\{ \matrix{
{x_G} = {{ – 3 + 9 – 5} \over 3} = {1 \over 3} \hfill \cr
{y_G} = {{6 – 10 + 4} \over 3} = 0 \hfill \cr} \right.\)
b)Tứ giác BGCD là hình bình hành thì tọa độ điểm D là \(D({{11} \over 3}; – 6)\)
Bài 1.46
Cho tam giác đều ABC cạnh a. Chọn hệ tọa độ \((O;\overrightarrow i ,\overrightarrow j )\), trong đó O là trung điểm của cạnh BC, cùng hướng với , cùng hướng với .
a) Tính tọa độ của các đỉnh của tam giác ABC.
b) Tìm tọa độ trung điểm E của AC.
c) Tìm tọa độ tâm đường tròn ngoại tiếp tam giác ABC.

Advertisements (Quảng cáo)
(Xem h.160)
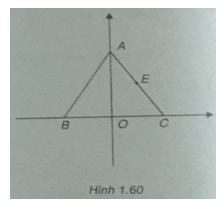
a) Ta có: Tam giác ABC cạnh a mà B là trung điểm BC nên \(OC = OB = {a \over 2}\)
\( \Rightarrow C\left( {{a \over 2};0} \right)$ và $B\left( { – {a \over 2};0} \right)\)
\(\eqalign{
& AO = \sqrt {{\rm{AC}}_{}^2 – {\rm{OC}}_{}^2} = \sqrt {a_{}^2 – \left( {{a \over 2}} \right)_{}^2} \cr
& = {{a\sqrt 3 } \over 2} \Rightarrow {\rm{A}}\left( {0;{{a\sqrt 3 } \over 2}} \right) \cr} \)
b) E là trung điểm AC
\( \Rightarrow \left\{ \matrix{
x_{\rm{E}}^{} = {{x_{\rm{A}}^{} + x_{\rm{C}}^{}} \over 2} = {a \over 4} \hfill \cr
y_{\rm{E}}^{} = {{y_{\rm{A}}^{} + y_{\rm{C}}^{}} \over 2} = {{a\sqrt 3 } \over 4} \hfill \cr} \right.\)
c) Do tam giác ABC đều nên tâm đường tròn ngoại tiếp tam giác trùng với trọng tâm G.
\(\left\{ \matrix{
x_{\rm{G}}^{} = {{x_{\rm{A}}^{} + x_{\rm{B}}^{} + x_{\rm{C}}^{}} \over 3} = 0 \hfill \cr
y_{\rm{G}}^{} = {{y_{\rm{A}}^{} + y_{\rm{B}}^{} + y_{\rm{C}}^{}} \over 3} = {{a\sqrt 3 } \over 6} \hfill \cr} \right.\)
Bài 1.47
Cho lục giác ABCDEF. Chọn hệ tọa độ \((O;\overrightarrow i ,\overrightarrow j )\), trong đó O là tâm của lục giác đều, hai véc tơ \(\overrightarrow i \) và \(\overrightarrow {OD} \) cùng hướng, \(\overrightarrow j \) và \(\overrightarrow {EC} \) cùng hướng . Tính tọa độ các đỉnh của lục giác biết độ dài của lục giác là 6.

(h.161)
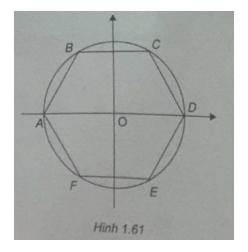
Do ABCDEF là lục giác đều nên \(AD = 2BC = 12 \Rightarrow AO = OD = 6\)
\( \Rightarrow A( – 6;0),D(6;0)\)
Gọi C’ là hình chiếu của C trên Ox
\(\eqalign{
& \Rightarrow OC’ = DC’ = 3 \cr
& \Rightarrow CC’ = \sqrt {CD_{}^2 – DC'{}^2} = \sqrt {6_{}^2 – 3_{}^2} = 3\sqrt 3 \cr} \)
\( \Rightarrow C(3;3\sqrt 3 )\)
B đối xứng với C qua Oy nên \(B( – 3;3\sqrt 3 )\)
E đối xứng với C qua Ox nên \(E(3; – 3\sqrt 3 )\)
F đối xứng với C qua O nên \(F( – 3; – 3\sqrt 3 )\)

