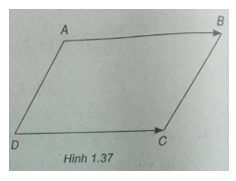
Bài 1.5: Cho tứ giác ABCD, chứng minh rằng \(\overrightarrow {AB} = \overrightarrow {DC} \) thì \(\overrightarrow {AD} = \overrightarrow {BC} \)

(h. 1.37)
Tứ giác ABCD có \(\overrightarrow {AB} = \overrightarrow {DC} \) nên AB = DC và AB // DC. Do đó ABCD là hình bình hành, suy ra:
\(\overrightarrow {AD} = \overrightarrow {BC} \)
Bài 1.6: Xác định vị trí tương đối của ba điểm phân biệt A, B và C trong các trường hợp sau:
a) \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) cùng hướng, \(\left| {\overrightarrow {AB} } \right| > \left| {\overrightarrow {AC} } \right|\)
b) \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) ngược hướng;
c) \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) cùng phương.
Advertisements (Quảng cáo)

a) Nếu \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) cùng hướng, \(\left| {\overrightarrow {AB} } \right| > \left| {\overrightarrow {AC} } \right|\) thì điểm C nằm giữa hai điểm A và B (h.1.38)

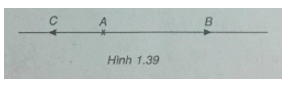
b) Nếu \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) ngược hướng thì điểm A nằm giữa hai điểm B và C (h. 1.39)
c) Nếu \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) cùng phương thì chúng có thể cùng hướng hoặc ngược hướng.
Advertisements (Quảng cáo)
Trường hợp \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) cùng hướng
– Nếu \(\left| {\overrightarrow {AB} } \right| > \left| {\overrightarrow {AC} } \right|\) thì C nằm giữa A và B.
– Nếu \(\left| {\overrightarrow {AB} } \right| < \left| {\overrightarrow {AC} } \right|\) thì B nằm giữa A và C.
Trường hợp Trường hợp \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) ngược hướng thì A nằm giữa B và C.
Bài 1.7: Cho hình bình hành ABCD. Dựng \(\overrightarrow {AM} = \overrightarrow {BA} \), \(\overrightarrow {MN} = \overrightarrow {DA} \), \(\overrightarrow {NP} = \overrightarrow {DC} \), \(\overrightarrow {PQ} = \overrightarrow {BC} \). Chứng minh \(\overrightarrow {AQ} = \overrightarrow 0 \)

(h.1.40)
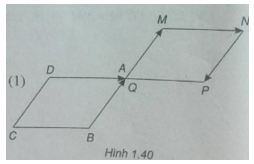
\(\overrightarrow {AM} = \overrightarrow {BA} \)
\(\overrightarrow {NP} = \overrightarrow {DC} = \overrightarrow {AB} \)
Suy ra AM = NP và AM // NP. Vậy tứ giác AMNP là hình bình hành. (1)
Ta có \(\overrightarrow {PQ} = \overrightarrow {BC} \)
\(\overrightarrow {MN} = \overrightarrow {DA} = \overrightarrow {CB} \)
Suy ra PQ = MN và P Q // MN . Vậy tứ giác MNPQ là hình bình hành (2).
Từ (1) và (2) suy ra A = Q hay \(\overrightarrow {AQ} = \overrightarrow 0 \)

