Bài 1.1: Hãy tính số các vec tơ (khác \(\overrightarrow 0 \)) mà các điểm đầu và điểm cuối được lấy từ các điểm phân biệt đã cho trong các trường hợp sau:
a) Hai điểm
b) Ba điểm;
c) Bốn điểm.

a)Với hai điểm A, B có hai vec tơ \(\overrightarrow {AB} ,\overrightarrow {BA} \)
b)Với ba điểm A, B, C có 6 vec tơ \(\overrightarrow {AB} ,\overrightarrow {BA} ,\overrightarrow {AC} ,\overrightarrow {CA} ,\overrightarrow {BC} ,\overrightarrow {CB} \)
c)Với bốn điểm A, B, C, D có 12 véc tơ (học sinh tự liệt kê).
Bài 1.2: Cho hình vuông ABCD có tâm O. Liệt kê tất cả các vec tơ bằng nhau (khác \(\overrightarrow 0 \)) nhận đỉnh và tâm của hình vuông làm điểm đầu và điểm cuối.

Advertisements (Quảng cáo)
(h 1.34)
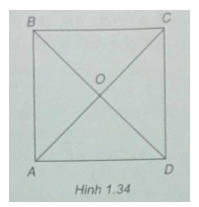
\(\overrightarrow {BC} = \overrightarrow {AD} ,\overrightarrow {CB} = \overrightarrow {DA} \)
\(\overrightarrow {AB} = \overrightarrow {DC} ,\overrightarrow {BA} = \overrightarrow {CD} \)
\(\overrightarrow {OB} = \overrightarrow {DO} ,\overrightarrow {BO} = \overrightarrow {OD} \)
\(\overrightarrow {AO} = \overrightarrow {OC} ,\overrightarrow {CO} = \overrightarrow {OA} \)
Advertisements (Quảng cáo)
Bài 1.3: Cho tứ giác ABCD. Gọi M, N, P và Q lần lượt là trung điểm của các cạnh AB, BC, CD và DA. Chứng minh \(\overrightarrow {NP} = \overrightarrow {MQ} \) và \(\overrightarrow {PQ} = \overrightarrow {NM} \)

(h. 1.35)
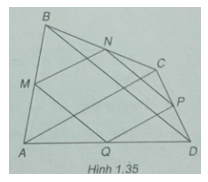
MN = PQ và MN // PQ
Vì chúng đều bằng \({1 \over 2}\) AC và đều song song với AC .
Vậy tứ giác MNPQ là hình bình hành nên ta có:
\(\overrightarrow {NP} = \overrightarrow {MQ} ,\overrightarrow {PQ} = \overrightarrow {NM} \)
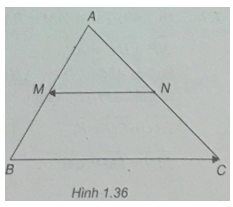
Bài 1.4: Cho tam giác ABC. Các điểm M và N lần lượt là trung điểm của các cạnh AB và AC. So sánh độ dài của hai vec tơ \(\overrightarrow {NM} \) và \(\overrightarrow {BC} \). Vì sao có thể nói hai vec tơ này cùng phương?

(h. 1. 36)
MN // BC và \(MN = {1 \over 2}BC\) hay \(\left| {\overrightarrow {MN} } \right| = {1 \over 2}\left| {\overrightarrow {BC} } \right|\)
Vì MN // BC nên \(\overrightarrow {NM} \) và \(\overrightarrow {BC} \) cùng phương.