Bài VII.5, VII.6, VII.7, VII.8 trang 94 sách bài tập Vật lý 11: Xác định ảnh S1’ tạo bởi Ll ?

VII.5. Trong công thức về số bội giác của kính hiển vi ngắm chừng ở vô cực  \({G_\infty } = {{\delta {\rm{D}}} \over {{f_1}{f_2}}}\) thì đại lượng  \(\delta\)  là gì?

A. Chiều dài của kính.

B. Khoảng cách F₁’F₂

C. Khoảng cực cận của mắt người quan sát.

D. Một đại lượng khác A, B, C

Đáp án B

VII.6. Công thức về số bội giác G = f₁/f₂ của kính thiên văn khúc xạ áp dụng được cho trường hợp ngắm chừng nào?

A. Ở điểm cực cận

B. Ở điểm cực viễn.

C. Ở vô cực (hệ vô tiêu)

D. Ở mọi trường hợp ngắm chừng vì vật luôn ở vô cực.

Đáp án C

Bài VII.7: Một thấu kính hội tụ có tiêu cự f.  Đặt thấu kính này giữa vật AB và màn (song song với vật) sao cho ảnh của AB hiện rõ trên màn và gấp hai lần vật.  Để ảnh rõ nét của vật trên màn gấp ba lần vật, phải tăng khoảng cách vật – màn thêm 10 cm. Tính tiêu cự f của thấu kính.

Theo đề bài: k₁ = -2 –> – d­₁’/d₁ = -2 –> d₁’ = 2d₁

Ta cũng có:

\({k_1} = {f \over {f – {d_1}}} = – 2 \Rightarrow {d_1} = {{3f} \over 2}\)

Vậy L₁ = d₁ + d₁’ = 9f/2

Xem Hình VII.1G.

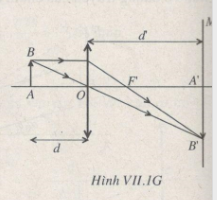
Tương tự: k₂ = -3 –> L₂ = d₂ + d₂’ = 16f/3

Do đó: L₂ – L₁ = 10cm –> 5f/6 = 10cm –> f = 12cm.

Bài VII.8: Một thấu kính phân kì L₁ có tiêu cự f = -20 cm. S là điểm sáng ở vô cực trên trục chính.

a) Xác định ảnh S₁’ tạo bởi L_l

b) Ghép thêm thấu kính hội tụ L₂ sau L₁ đồng trục. Sau L₂ đặt một màn vuông góc với trục chính chung và cách L₁ một đoạn 100 cm.

Khi tịnh tiến L₂, chỉ có một vị trí duy nhất của L₂ tạo ảnh sau cùng rõ nét trên màn. Tính f₂.

a) d₁ –> ∞; d₁’ = f₁ = -20cm

b)

Khi S₂’ hiện trên màn (Hình VII.2G) ta có:

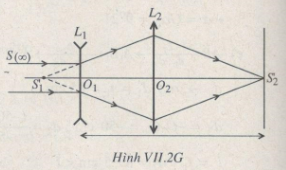
d₂ + d₂’ = l + |f₁| = L = const

\(\eqalign{
& \Rightarrow {d_2} + {{{d_2}{f_2}} \over {{d_2} – {f_2}}} = L \cr
& \Rightarrow d_2^2 – L{d_2} + L{f_2} = 0 \cr} \)

Vì chỉ có một vị trí của L₂ nên phương trình trên có nghiệm kép.

\(\eqalign{
& \Delta = {L^2} – 4L{f_2} = 0 \cr
& \Rightarrow {f_2} = {L \over 4} = {{120} \over 4} = 30cm \cr} \)