Bài IV.5: Một ống dây dẫn hình trụ dài 85 cm (không lõi sắt) gồm 750 vòng dây, trong đó có dòng điện cường độ 5,6 A. Xác định cảm ứng từ bên trong ống dây dẫn.
Áp dụng công thức: B = 4π.10-7NI/l ta tìm được cảm ứng từ bên trong ống dây dẫn:
\(B = {4.3,14.10^{ – 7}}.{{750} \over {{{85.10}^{ – 2}}}}.5,6 = {6,2.10^{ – 3}}T\)
Bài IV.6: Một prôtôn có vận tốc đầu v0 = 0, được gia tốc qua hiệu điện thế 100 V. Sau đó, prôtôn bay vào một từ trường đều theo hướng vuông góc với các đường sức từ. Khi đó quỹ đạo của prôtôn là đường tròn có bán kính 30 cm. Nếu thay thế prôtôn bằng hạt α với cùng những điều kiện ban đầu như trên thì bán kính quỹ đạo của hạt α bằng bao nhiêu ? Hạt a là hạt nhân heli\({}_2^4He\) có điện tích 3,2.10-19 C và khối lượng 6,642.10-27 kg. Prôtôn có điện tích 1,6.10-19 C và khối lượng l,672.10-27 kg.
Sau khi được gia tốc qua hiệu điện thế U, hạt điện tích q sẽ có vận tốc \(\overrightarrow v \) tính bằng :
\({{m{v^2}} \over 2} = |q|U \Rightarrow v = \sqrt {{{2|q|U} \over m}} \)
Quỹ đạo của hạt điện tích q có vận tốc \(\overrightarrow v \) bay vào từ trường đều B theo hướng vuông góc với các đường sức từ, là đường tròn nằm trong mặt phẳng vuông góc với từ trường và có bán kính :
\(R = {{mv} \over {|q|B}} = {1 \over B}.\sqrt {{{2mU} \over {|q|}}} \)
Với hạt proton: \({R_1} = {1 \over B}.\sqrt {{{2{m_1}U} \over {|{q_1}|}}} \) , với hạt α: \({R_2} = {1 \over B}.\sqrt {{{2{m_2}U} \over {|{q_2}|}}} \)
So sánh bán kính quỹ đạo của hai hạt điện tích trên ta tìm được:
\({{{R_2}} \over {{R_1}}} – \sqrt {{{{m_2}} \over {{m_1}}}} .\sqrt {{{|{q_1}|} \over {|{q_2}|}}} = \sqrt {{{6,642} \over {1,672}}} .\sqrt {{{{{1,6.10}^{ – 19}}} \over {{{3,2.10}^{ – 19}}}}} \approx 1,41\)
Advertisements (Quảng cáo)
Từ đó suy ra bán kính quỹ đạo của hạt α:
R2 = 1,41R1 = 1,41. 30= 42,3 cm.
Bài IV.7: Cho hai dòng điện có cùng cường độ 8 A chạy trong hai dây dẫn thẳng dài, đặt vuông góc với nhau, cách nhau một khoảng 8,0 cm trong chân không : dây dẫn thứ nhất thẳng đứng có dòng điện chạy từ dưới lên trên, dây dẫn thứ hai thẳng ngang có dòng điện chạy từ trái qua phải. Xác định cảm ứng từ tại trung điểm của khoảng cách giữa hai dây dẫn này.
Khoảng cách giữa hai dây dẫn thẳng có dòng điện I1 và I2 là đoạn thẳng CD = d = 8,0 cm nằm trong cùng mặt phẳng ngang p chứa dòng điện I2.
Hai vectơ cảm ứng từ \(\overrightarrow {{B_1}} \) và \(\overrightarrow {{B_2}} \) lần lượt do I1 và I2 gây ra tại trung điểm M của đoạn CD có hướng như trên Hình IV. 1G:
\(\overrightarrow {{B_1}} \) song song với dây dẫn có dòng điện I2 và cùng chiều với I2, \(\overrightarrow {{B_2}} \) song song với dây dẫn có dòng điện I1 và cùng chiều với I1, có độ lớn bằng nhau
\({B_1} = {B_2} = {2.10^{ – 7}}.{{8,0} \over {{{4,0.10}^{ – 2}}}} = {4,0.10^{ – 5}}T\)
Advertisements (Quảng cáo)
Vecto cảm ứng từ tổng hợp tại điểm M:
\(\overrightarrow {{B}} \)= \(\overrightarrow {{B_1}} \)+ \(\overrightarrow {{B_2}} \)
Vì \(\overrightarrow {{B_1}} \bot \overrightarrow {{B_2}} \) nên độ lớn của \(\overrightarrow {{B}} \) tính bằng:
\(B = {B_1}\sqrt 2 = 4\sqrt 2 {.10^{ – 5}}T\)
Bài IV.8: Hai dòng điện có cường độ 4,0 A và 6,0 A chạy ngược chiều nhau trong hai dây dẫn thẳng dài song song, đặt cách nhau 5,0 cm trong không khí. Xác định lực từ tác dụng lên một đơn vị dài của mỗi dây dẫn có dòng điện chạy qua
Dòng điện I1 gây ra tại điểm M nằm trên dòng điện I2, cách I1một khoảng a = 5,0 cm một từ trường có cảm ứng từ \(\overrightarrow {{B_1}} \) hướng vuông góc với mặt phẳng (I1; I2) (Hình IV.2G) và có độ lớn
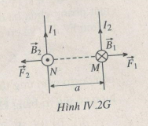
B1 = 2.10-7I1/a
Áp dụng quy tắc bàn tay trái, ta xác định được lực từ \(\overrightarrow {{F_1}} \) do \(\overrightarrow {{B_1}} \) tác dụng lên I2 là lực đẩy nằm trong mặt phẳng (I1; I2), hướng vuông góc với \(\overrightarrow {{B_1}} \) và I2, có độ lớn :
\({F_1} = {B_1}{I_2}\ell = {2.10^{ – 7}}.{{{I_1}} \over a}{I_2}\ell \)
Từ đó suy ra độ lớn của lực từ tác dụng lên một đơn vị dài của dây dẫn có dòng điện I2 :
\({F_{01}} = {{{F_1}} \over \ell } = {2.10^{ – 7}}.{{{I_1}} \over a}.{I_2}\)
Thay số, ta được :
\({F_{01}} = {2.10^{ – 7}}.{{4,0} \over {{{5.10}^{ – 2}}}}.6,0 = {9,6.10^{ – 5}}N\)
Lập luận tương tự như trên, ta xác định được lực từ \(\overrightarrow {{F_2}} \) do \(\overrightarrow {{B_2}} \) tác dụng lên I1 cũng là lực đẩy nằm trong mặt phẳng (I1; I2) hướng vuông góc với \(\overrightarrow {{B_2}} \) và I1, có độ lớn F2 = F1, tức là:
\({F_2} = {B_2}{I_1}\ell = {2.10^{ – 7}}.{{{I_2}} \over a}{I_1}\ell = {F_1}\)
Như vậy, lực từ tác dụng lên một đơn vị dài của dây dẫn có dòng điện I1 cũng có độ lớn
\({F_{02}} = {{{F_2}} \over \ell } = {2.10^{ – 7}}.{{{I_2}} \over a}.{I_1} = {9,6.10^{ – 5}}T = {F_{01}}\)

