33.4. Số bội giác của kính hiển vi ngắm chừng ở vô cực có (các) tính chất nào sau đây ?
A. Tỉ lệ thuận với tiêu cự vật kính.
B. Tỉ lệ thuận với tiêu cự thị kính.
C. Tỉ lệ thuận với độ dài quang học của kính.
D. Các kết luận A, B, C đều đúng.
Đáp án C
33.5. Trên vành vật kính và thị kính của kính hiển vi thường có ghi các con số. Nêu ý nghĩa của các con số này :
|
|
Vật kính |
Thị kính |
|
A. |
Số phóng đại ảnh |
Tiêu cự |
|
B. |
Số phóng đại ảnh |
Số bội giác ngắm chừng ở vô cực |
|
C. |
Tiêu cự |
Số phóng đại ảnh |
|
D. |
Tiêu cự |
Độ tụ |
Đáp án B
33.6. Kính hiển vi có f1 = 5 mm ; f2 = 2,5 cm ; d = 17 cm. Người quan sát có OCc = 20 cm. Số bội giác của kính ngắm chừng ở vô cực có trị số là :
A. 170. B. 272. C. 340. D. Khác A, B, C
Advertisements (Quảng cáo)
Đáp án B
Bài 33.7: Vật kính và thị kính của một kính hiển vi có tiêu cự lần lượt là f1 = l cm; f2 = 4 cm. Độ dài quang học của kính là d= 15 cm.
Người quan sát có điểm Cc cách mắt 20 cm và điểm Cv ở vô cực.
a) Hỏi phải đặt vật trong khoảng nào trước kính (mắt đặt sát kính) ?
b) Năng suất phân li của mắt người quan sát là ε = 1′. Tính khoảng cách nhỏ nhất giữa hai điểm của vật mà người quan sát còn phân biệt được khi ngắm chừng ở vô cực.
a) Khoảng có thể xê dịch vật MN tương ứng với khoảng CV CC có thể sẽ dịch ảnh.
\(M\xrightarrow[{{d_1};{d_1}’}]{{{L_1}}}{M_1}\xrightarrow[{{d_2};{d_2}’}]{{{L_2}}}M’ \equiv {C_V}\)
Advertisements (Quảng cáo)
\(\begin{gathered}
{d_2}’ = – O{C_V} \to \infty \hfill \\
{d_2} = {f_2} = 4cm \hfill \\
{d_1}’ = l – {d_2} = 20 – 4 = 16cm \hfill \\
{d_1} = \frac{{16.1}}{{15}} \approx 10,67mm \hfill \\
\end{gathered} \)
\(N\xrightarrow[{{d_1};{d_1}’}]{{{L_1}}}{N_1}\xrightarrow[{{d_2};{d_2}’}]{{{L_2}}}N’ \equiv {C_C}\)
\(\begin{gathered}
{d_2}’ = – {O_2}{C_C} = – 20cm \hfill \\
{d_2} = \frac{{20.4}}{{24}} = \frac{{10}}{3}cm \hfill \\
{d_1}’ = l – {d_2} = 20 – \frac{{10}}{3} = \frac{{50}}{3}cm \hfill \\
{d_1} = \frac{{100}}{{94}} \approx 10,64mm \hfill \\
\end{gathered} \)
Vậy Δd = 0,03mm ≈ 30µm.
b) Khi ngắm chừng ở vô cực, ảnh A1’B1’ của vật tạo bởi vật kính ở tại tiêu diện vật của thị kính (Hình 33.1G).
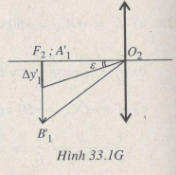
Khoảng ngắn nhất trên A1’B1’ mà mắt phân biệt được:
Δy1’ = f2tanε = f2ε
Suy ra khoảng ngắn nhất trên vật:
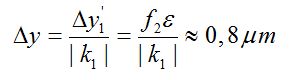
Bài 33.8: Kính hiển vi có vật kính L1 tiêu cự f1 = 0,8 cm và thị kính L2 tiêu cự f2 = 2 cm. Khoảng cách giữa hai kính là l = 16 cm.
a) Kính được ngắm chừng ở vô cực. Tính khoảng cách từ vật đến vật kính và số bội giác. Biết người quan sát có mắt bình thường với khoảng cực cận là OCc = 25 cm.
b) Giữ nguyên vị trí vật và vật kính, ta dịch thị kính một khoảng nhỏ để thu được ảnh của vật trên màn đặt cách thị kính 30 cm. Tính độ dịch chuyển của thị kính, xác định chiều dịch chuyển. Tính số phóng đại ảnh.
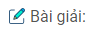
a) \(\eqalign{
& AB\mathrel{\mathop{\kern0pt\longrightarrow}
\limits_{{d_1};{d_1}’}^{{L_1}}} {A_1}{B_1}\mathrel{\mathop{\kern0pt\longrightarrow}
\limits_{{d_2};{d_2}’}^{{L_2}}} A’B’ \cr
& {d_2}’ \to \infty ;{d_2} = {f_2} = 2cm \cr
& {d_1}’ = l – {d_2} = 14cm;{d_1} = {{14.0,8} \over {13,2}} = 0,85cm = 8,5mm \cr
& {G_\infty } = {{\delta .O{C_C}} \over {{f_1}{f_2}}} = {{13,2.25} \over {0,8.2}} \approx 206 \cr}\)
b) \({d_2}’ = 30cm;{d_2} = {{30.2} \over {28}} \approx 2,14cm > 2cm\)
Dời ra vật kính đoạn Δd2 = 0,14cm = 1,4mm
Số phóng đại ảnh:
\(k = {k_1}{k_2} = {{{d_1}’} \over {{d_1}}}.{{{d_2}’} \over {{d_2}}} = 230,1\)

