Bài 29.12: Một thấu kính hội tụ có tiêu cự f = 20cm. Tìm vị trí của vật trước thấu kính để ảnh của vật tạo bởi thấu kính gấp 4 lần vật.
Giải bài toán bằng hai phương pháp:
a) Tính toán.
b) Vẽ.
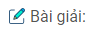
a) Giải bằng tính toán
Vật thật có thể có ảnh thật hoặc ảnh ảo qua thấu kính hội tụ
* Ảnh thật:
\({k_1} = \frac{f}{{f – d}} = – 4 \Rightarrow d = \frac{{5f}}{4} = \frac{{5.20}}{4} = 25cm\)
* Ảnh ảo:
\({k_2} = \frac{f}{{f – d}} = 4 \Rightarrow d = \frac{{3f}}{4} = \frac{{3.20}}{4} = 15cm\)
b) Giải bằng phép vẽ:
* Ảnh thật:
Ảnh ngược chiều so với vật và bằng 4 lần vật (Hình 29.1G)
– Lấy trên thấu kính \(\overline {{\rm{OJ}}} = – 4\overline {OI} \)
– Kẻ đường thẳng qua I song song với trục chính.
– Nối JF cắt đường thẳng trên tại B.
– Hạ BA vuông góc với trục chính.
AB là vị trí vật.
Tính đồng dạng cho:
Advertisements (Quảng cáo)
FA = 5cm à OA = 25cm
* Ảnh ảo:
Ảnh cùng chiều so với vật. Thực hiện cách vẽ tương tự (HÌnh 29.2G) nhưng với \(\overline {{\rm{OJ}}} = 4\overline {OI} \)
Ta có FA = 5cm; OA = 20 – 5 = 15cm.
Bài 29.13: Thấu kính hội tụ có tiêu cự f= 20 cm. Vật AB trên trục chính, vuông góc với trục chính có ảnh A’B’ cách vật 18 cm.
a) Xác định vị trí của vật.
b) Xác định ảnh, vẽ ảnh.
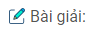
a) Trong mọi trường hợp (Hình 29.3G):
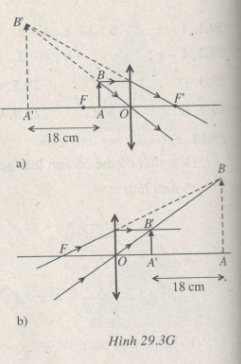
AA’ = |d + d’|
Do đó theo đề bài: |d + d’| = 18cm
Với \(d’ = \frac{{df}}{{d – f}} = \frac{{20d}}{{d – 20}}\)
Advertisements (Quảng cáo)
ta suy ra:
\(\begin{array}{l}
d + \frac{{20d}}{{d – 20}} = \pm 18\\
\Rightarrow {d^2} \pm 8d \mp 360 = 0
\end{array}\)
* d2 – 18d + 360 = 0: phương trình vô nghiệm.
* d2 + 18d – 360 = 0: có hai nghiệm.
Hai vị trí của vật:
d1 = 12cm; d2 = -30cm.
Chú ý: Phương trình d2 – 18d + 360 = 0 ứng với vật thật – ảnh thật.
Ta biết khi đó AA’min = 4f = 80cm
Do đó trị số AA’ = 18cm không phù hợp.
b) – Với d1 = 12cm: ảnh ảo à : d1’ = -30cm
– Với d2 = -30cm: vật ảo à d2’ = 12cm (không xét).
Bài 29.14: Thấu kính phân kì tạo ảnh ảo bằng 1/2 vật thật và cách vật 10 cm.
a) Tính tiêu cự của thấu kính.
b) Vẽ đường đi của một chùm tia sáng minh hoạ sự tạo ảnh.
a) Tiêu cự:
Vật thật có ảnh ảo –> k = -d’/d = ½; d’ = -d/2.
Theo đề ra: d + d’ = 10cm
–> d = 20cm; d’ = -10cm
\(f = \frac{{{\rm{dd}}’}}{{d + d’}} = – 20cm\)
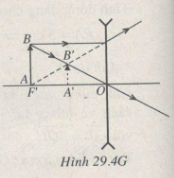
b) Đường truyền của chùm tia sáng
Xem Hình 29.4G
Bài 29.15: Vật phẳng nhỏ AB đặt trước và song song với một màn, cách màn khoảng L. Đặt một thấu kính hội tụ giữa vật và màn, song song với vật sao cho điểm A của vật ở trên trục chính. Ta tìm được hai vị trí O1; O2 của thấu kính tạo ảnh rõ nét của vật trên màn, ảnh này gấp k lần ảnh kia.
Tính tiêu cự của thấu kính.
Áp dụng bằng số : L = 100 cm ; k = 2,25
Theo giả thiết: d2 = d1’; d2’ = d1; \(\frac{{\overline {{A_2}'{B_2}’} }}{{\overline {{A_1}'{B_1}’} }} = \frac{{{k_2}}}{{{k_1}}} = k\)
Suy ra: \({\left( {\frac{{{d_1}}}{{{d_1}’}}} \right)^2} = k \Rightarrow \frac{{{d_1}}}{{{d_1}’}} = \sqrt k \)
Do đó:
\(\begin{array}{l}
\frac{{{d_1}}}{{\sqrt k }} = \frac{{{d_1}’}}{1} = \frac{L}{{1 + \sqrt k }} \Rightarrow \frac{1}{f} = \frac{{1 + \sqrt k }}{L} + \frac{{1 + \sqrt k }}{{L\sqrt k }}\\
f = \frac{{L\sqrt k }}{{{{(1 + \sqrt k )}^2}}}
\end{array}\)
Áp dụng bằng số: f = 24cm.

