Bài 28.7: Lăng kính có chiết suất n = 1,50 và góc chiết quang A = 30°. Một chùm tia sáng hẹp, đơn sắc được chiếu vuông góc đến mặt trước của lăng kính,
a) Tính góc ló và góc lệch của chùm tia sáng.
b) Giữ chùm tia tới cố định, thay lăng kính trên bằng một lăng kính có cùng kích thước nhưng có chiết suất n’ \( \ne \) n. Chùm tia ló sát mật sau của lăng kính. Tính n’.
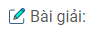
a) Ở I: i = 0 => r = 0.
Tia sáng truyền thẳng vào lăng kính (Hình 28.1G). Ở J : iJ = 30° (góc có cạnh tương ứng vuông góc) :
\({\mathop{\rm s}\nolimits} {\rm{inr}} = n\sin {i_J} = \frac{3}{2}.\frac{1}{2} = 0,75 \Rightarrow r \approx {48^0}35’\)
Suy ra góc lệch :
D = r-iJ = 48°35′ – 30° = 18°35′
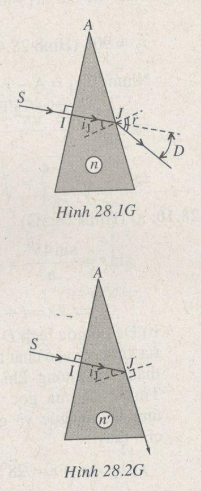
b) Ta có ở J trong trường hợp này (Hình 28.2G) :n’siniJ = sin900 à n’ = 1/sin300 = 2
a) Ở I: i = 0 => r = 0.
Tia sáng truyền thẳng vào lăng kính (Hình 28.1G). Ở J : iJ = 30° (góc có cạnh tương ứng vuông góc) :
Suy ra góc lệch :
D = r-iJ = 48°35′ – 30° = 18°35′
Advertisements (Quảng cáo)
b) Ta có ở J trong trường hợp này (Hình 28.2G) :
n’siniJ = sin900 à n’ = 1/sin300 = 2
Bài 28.8: Lăng kính có chiết suất n và góc chiết quang A. Một tia sáng đơn sắc được chiếu tới lăng kính sát mặt trước. Tia sáng khúc xạ vào lăng kính và ló ra ớ mặt kia với góc ló i’. Thiết lập hệ thức
\(\frac{{{\rm{cosA + sini’}}}}{{\sin A}} = \sqrt {{n^2} – 1} \)
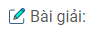
Ta có ở I (Hình 28.3G):
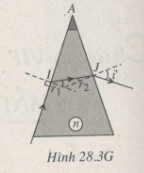
nsinr1 = sin900 –> sinr1 = 1/n
Mặt khác r1 + r2 = A à r2 = A – r1
Advertisements (Quảng cáo)
Ở J:
\(\begin{array}{l}
n\sin {r_2} = \sin i’\\
\Rightarrow n\sin (A – {r_1}) = \sin i’\\
\Rightarrow \sin A\cos {r_1} – {\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_1}{\rm{cosA = }}\frac{{\sin i’}}{n}\\
\Rightarrow \sin A\sqrt {1 – {{\sin }^2}_{{r_1}}} – {\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_1}{\rm{cosA = }}\frac{{\sin i’}}{n}\\
\Rightarrow \sin A\frac{{\sqrt {{n^2} – 1} }}{n} – \frac{{{\rm{cosA}}}}{n} = \frac{{\sin i’}}{n}
\end{array}\)
Do đó: \(\frac{{{\rm{cosA + sini’}}}}{{\sin A}} = \sqrt {{n^2} – 1} \)
Bài 28.9: Một lăng kính có tiết diện vuông góc là một tam giác đều ABC. Một chùm tia sáng đơn sắc hẹp SI được chiếu tới mặt AB trong mặt phẳng của tiết diện vuông góc và theo phương vuông góc với đường cao AH của ABC. Chùm tia ló khỏi mặt AC theo phương sát với mặt này. Tính chiết suất của lăng kính.
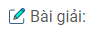
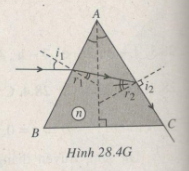
Theo đề bài: i = 300; sinr1 = 1/2n
i2 = 900 (HÌnh 28.4G); r2 = igh –> sinr2 = 1/n
Nhưng r1 = A – r2 – 600 – igh
\(\begin{array}{l}
\Rightarrow \frac{1}{{2n}} = \frac{{\sqrt 3 }}{2}.\frac{{\sqrt {{n^2} – 1} }}{n} – \frac{1}{n}.\frac{1}{2}\\
\Rightarrow n = \sqrt {1 + \frac{4}{3}} = \sqrt {\frac{7}{3}} \approx 1,53
\end{array}\)
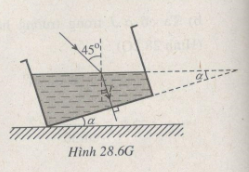
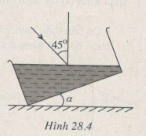
Bài 28.10: Chậu chứa chất lỏng có chiết suất n = l,5. Tia tới chiếu tới mặt thoáng với góc tới 45°
(Hình 28.4).
a) Tính góc lệch khi ánh sáng khúc xạ vào chất lỏng.
b) Tia tới cố định. Nghiêng đáy chậu một góc α. Tính α để có góc lệch giữa tia tới và tia ló có giá trị như ở câu a (coi bề dày trong suốt của đáy chậu không đáng kể).
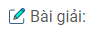
a) (Hình 28.5G)
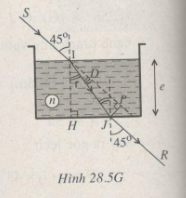
\({\mathop{\rm s}\nolimits} {\rm{inr}} = \frac{{\sin {{45}^0}}}{n} = \frac{1}{{1,5\sqrt 2 }} \Rightarrow r \approx {28^0}\)
–> D = I – r = 170
b) Để có góc lệch D như ở câu a thì tia khúc xạ vào chất lỏng phải truyền thẳng ra không khí (Hình 28.6G). Tính chất của góc có cạnh tương ứng vuông góc và góc so le trong cho thẩy α = r = 280.