Bài 4: Tìm cấp số nhân có sáu số hạng, biết rằng tổng của năm số hạng đầu là \(31\) và tổng của năm số hạng sau là \(62\).
Giả sử có cấp số nhân: \({u_1},{u_2},{u_3},{u_4},{u_5},{u_6}\)
Theo giả thiết ta có:
\({u_1} + {u_2} + {u_3} + {u_4} + {u_5} = 31\). (1)
\({u_2} + {u_3} + {u_4} + {u_5} + {u_6} = 62\). (2)
Nhân hai vế của (1) với \(q\), ta được: \({u_1}q + {u_2}q + {u_3}q + {u_4}q + {u_5}q = 31q\)
hay \({u_2} + {u_3} + {u_4} + {u_5} + {u_6} = 31q\)
Suy ra \(62 = 31.q\) hay \(q = 2\).
Advertisements (Quảng cáo)
Ta có \(S_5= 31 = {{{u_1}(1 – {2^5})} \over {1 – 2}}\) nên suy ra \(u_1= 1\).
Vậy ta có cấp số nhân \(1, 2, 4, 8, 16, 32\).
Bài 5: Tỉ lệ tăng dân số của tỉnh X là \(1,4\% \). Biết rằng số dân của tỉnh hiện nay là \(1,8\) triệu người. Hỏi với mức tăng như vậy thì sau 5 năm, 10 năm số dân của tỉnh đó là bao nhiêu?
 :
:
Giả sử số dân của một tỉnh đó hiện nay là \(N\). Vì tỉ lệ tăng dân số là \(1,4\%\) nên sau một năm, số dân tăng thêm là \(1,4\%.N\).
Advertisements (Quảng cáo)
Vậy số dân của tỉnh đó vào năm sau là
\(N + 1,4\%.N = 101,4\%.N =\) \( \frac{101,4}{100}.N\).
Như vậy số dân của tỉnh đó sau mỗi năm lập thành cấp số nhân.
\(N\), \( \frac{101,4}{100}.N\), \( (\frac{101,4}{100})^{2}.N\), …
Vậy nếu \(N = 1,8\) triệu người, áp dụng công thức tính số hạng tổng quát của cấp số nhân thì sau \(5\) năm số dân của tỉnh là \( (\frac{101,4}{100})^{5}.1,8 ≈ 1,9\) (triệu người)
và sau \(10\) năm sẽ là \( (\frac{101,4}{100})^{10}.1,8 ≈ 2,1\) (triệu người).
Bài 6: Cho hình vuông \(C_1\) có cạnh bằng \(4\). Người ta chia mỗi cạnh của hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông lại làm tiếp tục như trên để được hình vuông khác. Tiếp tục quá trình như trên, ta nhận được dãy các hình vuông. Gọi \(a_1\) là độ dài cạnh của hình vuông \(C_n\). Chứng minh dãy số \((a_n)\) là một cấp số nhân.
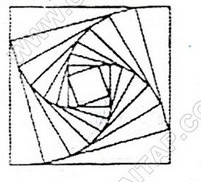
Xét dãy số \((a_n)\), ta có \(a_1= 4\).
Giả sử hình vuông cạnh \(C_n\) có độ dài cạnh là \(a_n\). Ta sẽ tính cạnh \(a_{n+1}\) của hình vuông \(C_{n+1}\) Theo hình 44, áp dụng định lí Pi-ta-go, ta có:
\({a_{n + 1}} = \sqrt {{{\left( {{1 \over 4}{a_n}} \right)}^2} + {{\left( {{3 \over 4}{a_n}} \right)}^2}} = {a_n}.{{\sqrt {10} } \over 4}\forall n \in {\mathbb N}^*\)
Vậy dãy số \((a_n)\) là cấp số nhân với số hạng đầu là \(a_1= 4\) và công bội \(q = {{\sqrt {10} } \over 4}\).

