Bài 1.11: Cho tứ giác ABCE. Dựng ảnh của tam giác ABC qua phép đối xứng tâm E.
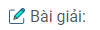
Dựng ảnh của từng điểm qua phép đối xứng tâm E ta được hình sau:
Bài 1.12: Trong mặt phẳng Oxy, cho hai điểm I(1; 2), M(-2; 3), đường thẳng d có phương trình \(3x – y + 9 = 0\) và đường tròn (C) có phương trình: \({x^2} + {y^2} + 2x – 6y + 6 = 0\)
Hãy xác định tọa độ của điểm M’, phương trình của đường thẳng d’ và đường tròn (C’) theo thứ tự là ảnh của M, d và (C) qua
a) Phép đối xứng qua gốc tọa độ;
b) Phép đối xứng qua tâm I.
Advertisements (Quảng cáo)
a) Gọi M’, d’ và (C’) theo thứ tự là ảnh của M, d và (C) qua phép đối xứng qua O. Dùng biểu thức tọa độ của phép đối xứng qua gốc tọa độ ta có :
\(M’ = \left( {2; – 3} \right)\), phương trình của \(d’:3{\rm{x}} – y – 9 = 0\), phương trình của đường tròn \(\left( {C’} \right):{x^2} + {y^2} – 2{\rm{x}} + 6y + 6 = 0\)
b) Gọi M’, d’ và (C’) theo thứ tự là ảnh của M, d và (C) qua phép đối xứng qua I .
Vì I là trung điểm của MM’ nên \(M’ = \left( {4;1} \right)\)
Advertisements (Quảng cáo)
Vì d’ song song với d nên d’ có phương trình \(3{\rm{x}} – y + C = 0\). Lấy một điểm trên d, chẳng hạn \(N\left( {0;9} \right)\). Khi đó ảnh của N qua phép đối xứng qua tâm I là \(N’\left( {2; – 5} \right)\). Vì N’ thuộc d nên ta có \(3.2 – \left( { – 5} \right) + C = 0\). Từ đó suy ra C = -11.
Vậy phương trình của d’ là \(3{\rm{x}} – y – 11 = 0\).
Để tìm (C’), trước hết ta để ý rằng (C) là đường tròn tâm \(J\left( { – 1;3} \right)\), bán kính bằng 2. Ảnh của J qua phép đối xứng qua tâm I là \(J’\left( {3;1} \right)\). Do đó (C’) là đường tròn tâm J’ bán kính bằng 2. Phương trình của (C’) là \({\left( {x – 3} \right)^2} + {\left( {y – 1} \right)^2} = 4\).
Bài 1.13: Trong mặt phẳng Oxy, cho đường thẳng d có phương trình: \(x – 2y + 2 = 0\) và d đường thẳng có phương trình: \(x – 2y – 8 = 0\). Tìm phép đối xứng tâm biến d thành d’ và biến trục Ox thành chính nó.
Giao của d và d’ với lần lượt là \(A\left( { – 2;0} \right)\) và \(A’\left( {8;0} \right)\). Phép đối xứng qua tâm cần tìm biến A thành A’ nên tâm đối xứng của nó là \(I = \left( {3;0} \right)\).
Bài 1.14: Cho ba điểm I, J, K không thẳng hàng. Hãy dựng tam giác ABC nhận I, J, K lần lượt là trung điểm của các cạnh BC, AB, AC
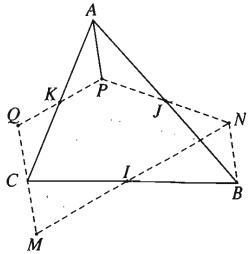
Giả sử tam giác ABC đã dựng được. Lấy điểm M bất kì. Gọi N là ảnh của M qua phép đối xứng tâm I. P là ảnh của N qua phép đối xứng tâm J. Q là ảnh của P qua phép đối xứng tâm K. Khi đó \(\overrightarrow {CM} = – \overrightarrow {BN} = \overrightarrow {AP} = – \overrightarrow {CQ} \). Do đó C là trung điểm của QM. Từ đó suy ra cách dựng tam giác ABC.
