Bài 1.9: Cho hai đường thẳng c, d cắt nhau và hai điểm A, B không thuộc hai đường thẳng đó. Hãy dựng điểm C trên c , điểm D trên d sao cho tứ giác ABCD là hình thang cân nhận AB là một cạnh đáy ( không cần biện luận ).
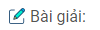
Ta thấy rằng B, C theo thứ tự là ảnh của A, D qua phép đối xứng qua đường trung trực của cạnh AB, từ đó suy ra cách dựng:
– Dựng đường trung trực ∆ của đoạn ab
Advertisements (Quảng cáo)
– Dựng d’ là ảnh của d qua phép đối xứng qua trục ∆.
Gọi \(C = d’ \cap c\).
– Dựng D là ảnh của C qua phép đối xứng qua trục ∆:
Advertisements (Quảng cáo)
Bài 1.10: Cho đường thẳng d và hai điểm A, B không thuộc d nhưng nằm cùng phía đối với d. Tìm trên d điểm M sao cho tổng các khoảng cách từ đó đến A và B là bé nhất.
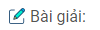
Gọi B’ là ảnh của B qua phép đối xứng qua trục d. Khi đó với mỗi điểm M thuộc d
\(MA + MB = MA + MB’\) nên \(MA + MB’\) bé nhất \( \Leftrightarrow A,M,B’\) thẳng hàng.
Tức là \(M = \left( {AB’} \right) \cap d\).

