Bài 1.6: Trong mặt phẳng tọa độ Oxy, cho điểm M(3; -5), đường thẳng d có phương trình \(3x + 2y – 6 = 0\) và đường tròn (C) có phương trình \({x^2} + {y^2} – 2x + 4y – 4 = 0\). Tìm ảnh của M, d, và (C) qua phép đối xứng qua trục Ox
Gọi \(M’,d’\) và (C’) theo thứ tự là ảnh của M, d và (C) qua phép đối xứng qua trục Ox . Khi đó \(M’ = \left( {3;5} \right)\) . Để tìm ta viết biểu thức tọa độ của phép đối xứng qua trục
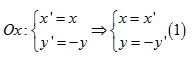
Thay (1) vào phương trình của đường thẳng d ta được \(3x’ – 2y’ – 6 = 0\). Từ đó suy ra phương trình của d’ là \(3x – 2y – 6 = 0\)
Thay (1) vào phương trình của (C) ta được \(x{‘^2} + y{‘^2} – 2{\rm{x}}’ + 4y’ – 4 = 0\) . Từ đó suy ra phương trình của (C’) là \({\left( {x – 1} \right)^2} + {\left( {y – 2} \right)^2} = 9\)
Cũng có thể nhận xét (C) có tâm là \(I\left( {1; – 2} \right)\) ,bán kính bằng 3,từ đó suy ra tâm I’ của (C’) có tọa độ (1; 2) và phương trình của (C’) là \({\left( {x – 1} \right)^2} + {\left( {y – 2} \right)^2} = 9\)
Advertisements (Quảng cáo)
Bài 1.7: Trong mặt phẳng Oxy cho đường thẳng d có phương trình \(x – 5y + 7 = 0\) và đường thẳng d’ có phương trình \(5x – y – 13 = 0\). Tìm phép đối xứng trục biến d thành d’.
Dễ thấy d và d’ không song song với nhau. Do đó trục đối xứng \(\Delta \) của phép đối xứng biến d thành d’ chính là đường phân giác của góc tạo bởi d và d’ . Từ đó suy ra \(\Delta \) có phương trình:
\(\eqalign{
& {{\left| {x – 5y + 7} \right|} \over {\sqrt {1 + 25} }} = {{\left| {5{\rm{x}} – y – 13} \right|} \over {\sqrt {25 + 1} }} \cr
& \Leftrightarrow x – 5y + 7 = \pm \left( {5{\rm{x}} – y – 13} \right) \cr} \)
Advertisements (Quảng cáo)
Từ đó tìm được hai phép đối xứng qua các trục:
\(\Delta_1 \) có phương trình \(x + y – 5 = 0\), \(\Delta_2 \) có phương trình \(x – y – 1 = 0\).
Bài 1.8: Tìm các trục đối xứng của hình vuông
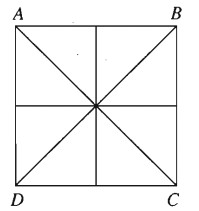
Cho hình vuông ABCD. Gọi F là phép đối xứng trục d biến hình vuông đó thành chính nó. Lí luận tương tự, ta thấy A chỉ có thể biến thành các điểm A, B, C hoặc D
– Nếu A biến thành chính nó thì C chỉ có thể biến thành chính nó và B biến thành D. Từ đó suy ra F là phép đối xứng qua trục AC
– Nếu A biến thành B thì d là đường trung trực của AB. Khi đó C biến thành D.
Các trường hợp khác lập luận tương tự. Do đó hình vuông ABCD có bốn trục đối xứng là các đường thẳng AC, BD và các đường trung trực của AB và BC.

