Bài 1.4: Trong mặt phẳng Oxy cho đường tròn (C) có phương trình \({x^2} + {y^2} – 2x + 4y – 4 = 0\). Tìm ảnh của (C) qua phép tịnh tiến theo vectơ \(\overrightarrow v = \left( { – 2;5} \right)\).
Cách 1. Dễ thấy (C) là đường tròn tâm \(I\left( {1; – 2} \right)\), bán kính \(r = 3\).Gọi \(I’ = {T_{\overrightarrow v }}\left( I \right) = \left( {1 – 2; – 2 + 5} \right) = \left( { – 1;3} \right)\) và (C’) là ảnh của (C) qua \({T_{\overrightarrow v }}\) thì (C’) là đường tròn tâm (I’) bán kính \(r = 3\). Do đó (C’) có phương trình:
\({\left( {x + 1} \right)^2} + {\left( {y – 3} \right)^2} = 9\)
Cách 2. Biểu thức tọa độ của \({T_{\overrightarrow v }}\) là
Advertisements (Quảng cáo)
\(\left\{ \matrix{
x’ = x – 2 \hfill \cr
y’ = y + 5 \hfill \cr} \right. \Rightarrow \left\{ \matrix{
x = x’ + 2 \hfill \cr
y = y’ – 5 \hfill \cr} \right.\)
Thay vào phương trình của (C) ta được
Advertisements (Quảng cáo)
\(\eqalign{
& {\left( {x’ + 2} \right)^2} + {\left( {y’ – 5} \right)^2} – 2\left( {x’ + 2} \right) + 4\left( {y’ – 5} \right) – 4 = 0 \cr
& \Leftrightarrow x{‘^2} + y{‘^2} + 2x’ – 6y’ + 1 = 0 \cr
& \Leftrightarrow {\left( {x’ + 1} \right)^2} + {\left( {y’ – 3} \right)^2} = 9 \cr} \)
Do đó (C’) có phương trình \({\left( {x + 1} \right)^2} + {\left( {y – 3} \right)^2} = 9\)
Bài 1.5: Cho đoạn thẳng AB và đường tròn (C) tâm O, bán kính r nằm về một phía của đường thẳng AB. Lấy điểm M trên (C), rồi dựng hình bình hành ABMM’. Tìm tập hợp các điểm M’ khi M di động trên (C).
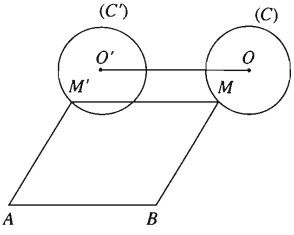
Do tứ giác ABMM’ là hình bình hành nên \(\overrightarrow {BA} = \overrightarrow {MM’} \) là. Từ đó suy ra M’ là ảnh của M qua phép tịnh tiến theo vectơ \(\overrightarrow {BA} \) .Từ đó suy ra tập hợp các điểm M’ là đường tròn (C’) , ảnh của C qua phép tịnh tiến theo vectơ \(\overrightarrow {BA} \) .

