Bài 3.5: Tìm đạo hàm của hàm số sau:
\(y = {\tan ^2}x – \cot {x^2}.\)
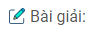
\(y’ = {{2\sin x} \over {{{\cos }^3}x}} + {{2x} \over {{{\sin }^2}{x^2}}}.\)
Bài 3.6: Tìm đạo hàm của hàm số sau:
\(f\left( t \right) = {{\cos t} \over {1 – \sin t}}\) tại \(t = {\pi \over 6}.\)
Advertisements (Quảng cáo)
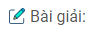
\(f’\left( t \right) = {{ – \sin t\left( {1 – \sin t} \right) + {{\cos }^2}t} \over {{{\left( {1 – \sin t} \right)}^2}}} = {1 \over {1 – \sin t}}\) ;
Do đó \(f’\left( {{\pi \over 6}} \right) = 2.\)
Advertisements (Quảng cáo)
Bài 3.7: Tìm đạo hàm của hàm số sau:
\(y = \sqrt x + {1 \over {\sqrt x }} + 0,1{x^{10}}.\)
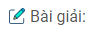
\(y’ = {1 \over {2\sqrt x }} – {1 \over {2x\sqrt x }} + {x^9}.\)
Bài 3.8: Tìm đạo hàm của hàm số sau:
\(y = {{2{x^2} + x + 1} \over {{x^2} – x + 1}}.\)
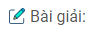
\(y’ = {{ – 3{x^2} + 2x + 2} \over {{{\left( {{x^2} – x + 1} \right)}^2}}}.\)

