Câu 132: Chứng minh rằng trung điểm bốn cạnh của một hình chữ nhật là đỉnh của một hình thoi.
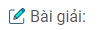
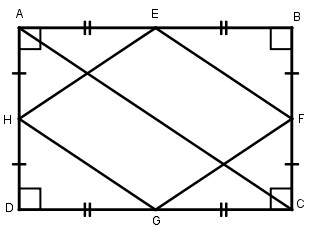
Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA của hình chữ nhật ABCD.
Kẻ đường chéo AC.
– Trong ∆ ABC ta có:
E là trung điểm của AB
F là trung điểm của BC
nên EF là đường trung bình của ∆ ABC
⇒ EF // AC và EF = \({1 \over 2}\)AC (tính chất đường trung bình tam giác) (1)
– Trong ∆ ADC ta có:
H là trung điểm AD
G là trung điểm DC
nên HG là đường trung bình của ∆ ADC.
⇒ HG // AC và HG = \({1 \over 2}\)AC (tính chất đường trung bình của tam giác) (2)
Từ (1) và (2) suy ra: EF // HG và EF = HG
Suy ra tứ giác EFGH là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
– Xét ∆ AEH và ∆ DGH:
AH = HG (gt)
\(\widehat {EAH} = \widehat {GDH} = {90^0}\)
AE = DG (vì AB = CD)
Do đó: ∆ AEH = ∆ DGH (c.g.c) ⇒ HE = HG
Vậy hình bình hành EFGH là hình thoi (vì có hai cạnh kề bằng nhau)
Câu 133: Chứng minh rằng trung điểm các cạnh của một hình thoi là đỉnh của một hình chữ nhật.
Advertisements (Quảng cáo)
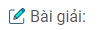
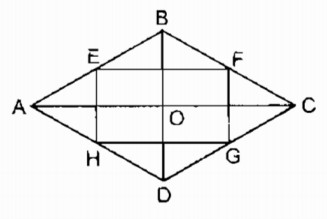
Giả sử hình thoi ABCD. Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA.
– Trong ∆ ABC ta có:
E là trung điểm của AB
F là trung điểm của BC
nên EF là đường trung bình của tam giác ABC.
⇒ EF // AC và EF = \({1 \over 2}\)AC (tính chất đường trung bình của tam giác) (1)
– Trong ∆ ADC ta có:
H là trung điểm của AD
G là trung điểm của CD
nên HG là đường trung bình của ∆ ADC
⇒ HG // AC và HG = \({1 \over 2}\)AC ( tính chất đường trung bình của tam giác) (2)
Từ (1) và (2) suy ra: EF // HG và EF = HG
Suy ra tứ giác EFGH là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
Mặt khác: AC ⊥ BD (tính chất hình thoi)
Advertisements (Quảng cáo)
EF // AC (chứng minh trên)
Suy ra: EF ⊥ BD
Trong ∆ ABD ta có EH là đường trung bình
⇒ EH // BD (tính chất đường trung bình của tam giác)
Suy ra: EH ⊥ EF hay = 1v
Vậy hình bình hành EFGH là hình chữ nhật.
Câu 134: Chứng minh rằng trong hình thoi:
a. Giao điểm của hai đường chéo là tâm đối xứng của hình thoi
b. Hai đường chéo là hai trục đối xứng của hình thoi.
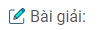
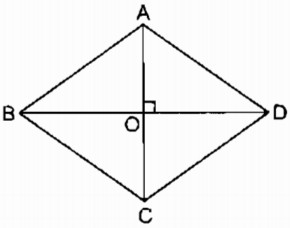
a. Hình bình hành có tâm đối xứng là giao điểm của hai đường chéo. Hình thoi cũng là một hình bình hành nên cũng có tâm đối xứng là giao điểm hai đường chéo của nó.
b. Ta có: AC ⊥ BD (tính chất hình thoi)
OB = OD ( tính chất hình thoi)
nên AC là đường trung trực của BD.
Do đó điểm đối xứng với điểm B qua AC là điểm D
Điểm đối xứng với điểm A qua AC là điểm A
Điểm đối xứng với điểm C qua AC là điểm C
Vậy điểm đối xứng với mỗi đỉnh của hình thoi qua AC cũng thuộc hình thoi.
Do đó AC là trục đối xứng của hình thoi ABCD.
OC = OA ( tính chất hình thoi)
nên BD là đường trung trực của AC
Do đó điểm đối xứng với điểm A qua BD là điểm C
Điểm đối xứng với điểm B qua BD là điểm B
Điểm đối xứng với điểm D qua BD là điểm D
Vậy điểm đối xứng với mỗi đỉnh của hình thoi qua BD cũng thuộc hình thoi.
Do đó BD là trục đối xứng của hình thoi ABCD.
Câu 135: Tứ giác ABCD có tọa độ các đỉnh như sau: A(0; 2), B( 3; 0), C(0; −2 ), D(−3; 0). Tứ giác ABCD là hình gì ? Tính chu vi của tứ giác đó ?
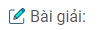
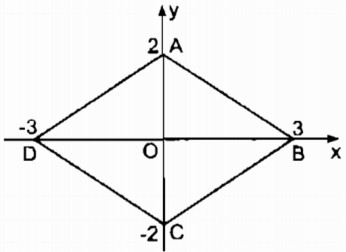
A(0; 2) và C(0; −2) nên hai điểm A và C đối xứng nhau qua O (0, 0) ⇒ OA = OC
B(3; 0) và D(−3; 0) nên hai điểm B và D đối xứng qua O (0; 0) ⇒ OB = OD
Tứ giác ABCD là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)
Ox ⊥ Oy hay AC ⊥ BD
Vậy tứ giác ABCD là hình thoi
Trong ∆ OAB vuông tại O. Theo định lý Pi-ta-go ta có:
\(\eqalign{ & A{B^2} = O{A^2} + O{B^2} \cr & A{B^2} = {2^2} + {3^2} = 4 + 9 = 13 \cr & AB = \sqrt {13} \cr} \)
Chu vi hình thoi bằng \(4\sqrt {13} \)

