Câu 121: Cho tam giác nhọn ABC, các đường cao BD, CE. Gọi H, K theo thứ tự là chân các đường vuông góc kẻ từ B, C đến đường thẳng DE. Chứng minh rằng EH = DH
HD: Vẽ điểm I là trung điểm của DE, điểm M là trung điểm của BC.
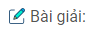
BH ⊥ DE (gt)
CK ⊥ DE (gt)
Suy ra BH // CK nên tứ giác BHKC là hình thang
Ta có: Gọi M là trung điểm của BC, I là trung điểm của DE
Trong tam giác BDC vuông tại D có DM là trung tuyến thuộc cạnh huyền BC.
⇒ DM = \({1 \over 2}\) BC (tính chất tam giác vuông)
Trong tam giác BEC vuông tại E có EM là đường trung tuyến thuộc cạnh huyền BC.
⇒ EM = ${1 \over 2}$BC (tính chất tam giác vuông)
Suy ra: DM = EM nên ∆ MDE cân tại M
MI là đường trung tuyến nên MI là đường cao ⇒ MI ⊥ DE
Suy ra: MI // BH // CK
BM = MC
Suy ra: HI = IK (tính chất đường trung bình hình thang)
⇒ HE + EI = ID + DK
mà EI = ID ( theo cách vẽ)
⇒ HE = DK
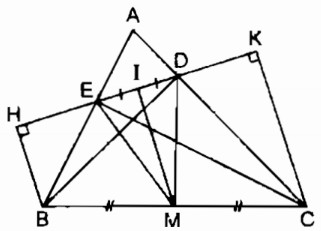
Câu 122: Cho tam giác ABC vuông tại A, đường cao AH. Gọi D, E theo thứ tự là chân các đường vuông góc kẻ từ H đến AB, AC.
a. Chứng minh rằng AH = DE.
Advertisements (Quảng cáo)
b. Gọi I là trung điểm của HB, K là trung điểm của HC. Chứng minh rằng DI // EK
a. Xét tứ giác ADHE:
\(\widehat A = {90^0}\) (gt)
\(\widehat {ADH} = {90^0}\) (vì HD ⊥ AB)
\(\widehat {AEH} = {90^0}\) (vì HE ⊥ AC)
Suy ra tứ giác ADHE là hình chữ nhật (vì có ba góc vuông)
⇒ AH = DE (tính chất hình chữ nhật)
b. ∆ BHD vuông tại D có DI là đường trung tuyến thuộc cạnh huyền BH
⇒ DI = IB = \({1 \over 2}\) BH (tính chất tam giác vuông)
⇒ ∆ IDB cân tại I \( \Rightarrow \widehat {DIB} = {{{{180}^0} – \widehat B} \over 2}\) (1)
∆ HEC vuông tại E có EK là đường trung tuyến thuộc cạnh huyền HC
Advertisements (Quảng cáo)
⇒ EK = KH = \({1 \over 2}\)HC (tính chất tam giác vuông)
⇒ ∆ KHE cân tại K \( \Rightarrow \widehat {EKH} = {{{{180}^0} – \widehat {KHE}} \over 2}\) (2)
Tứ giác ADHE là hình chữ nhật
⇒ HE // AD hay HE // AB
⇒ \(\widehat B = \widehat {KHE}\) (đồng vị) (3)
Từ (1), (2) và (3) suy ra: \(\widehat {DIB} = \widehat {EKH}\)
⇒ DI // EK (vì có cặp góc đồng vị bằng nhau).
Câu 123: Cho tam giác ABC vuông tại A, đường cao AH, đường trung tuyến AM.
a. Chứng minh rằng \(\widehat {HAB} = \widehat {MAC}\)
b. Gọi D, E theo thứ tự là chân các đường vuông góc kẻ từ H đến AB, AC. Chứng minh rằng AM vuông góc với DE.
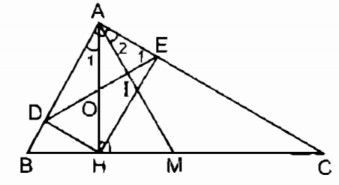
a. AH ⊥ BC (gt) \( \Rightarrow \widehat {HAB} + \widehat B = {90^0}\)
\(\widehat B + \widehat C = {90^0}\) (vì ∆ ABC có\(\widehat A = {90^0}\))
Suy ra: \(\widehat {HAB} = \widehat C\) (1)
∆ ABC vuông tại A có AM là trung tuyến thuộc cạnh huyền BC
⇒ AM = MC = \({1 \over 2}\) BC (tính chất tam giác vuông)
⇒ ∆ MAC cân tại M \( \Rightarrow \widehat {MAC} = \widehat C\) (tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra: \(\widehat {HAB} = \widehat {MAC}\)
b. xét tứ giác ADHE có:
\(\widehat A = {90^0}\) (gt)
\(\widehat {ADH} = {90^0}\) (vì HD ⊥ AB)
\(\widehat {AEH} = {90^0}\) (vì HE ⊥ AC)
Suy ra: Tứ giác ADHE là hình chữ nhật (vì có ba góc vuông)
⇒ ∆ ADH = ∆ EHD (c.c.c)
\( \Rightarrow {\widehat A_1} = \widehat {HED}\)
\(\widehat {HED} + {\widehat E_1} = \widehat {HEA} = {90^0}\)
Suy ra: \({\widehat E_1} + {\widehat A_1} = {90^0}\)
\({\widehat A_1} = {\widehat A_2}\) (chứng minh trên)
\( \Rightarrow {\widehat E_1} + {\widehat A_2} = {90^0}\)
Gọi I là giao điểm của AM và DE
Trong ∆ AIE ta có:
\(\widehat {AIE} = {180^0} – \left( {{{\widehat E}_1} + {{\widehat A}_1}} \right) = {180^0} – {90^0} = {90^0}\)
\(\Rightarrow \)AM ⊥ DE.

