Câu 96: Cho hình bình hành ABCD, O là giao điểm của hai đường chéo. Một đường thẳng đi qua O cắt hai cạnh đối AD, BC ở E, F. Chứng minh rằng các điểm E và F đối xứng nhau qua điểm O.
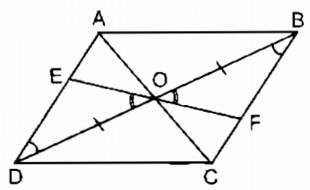
Xét ∆ OED và ∆ OFB:
\(\widehat {EOD} = \widehat {FOB}\) (đối đỉnh)
OD = OB (tính chất hình bình hành)
\(\widehat {ODE} = \widehat {OBF}\) (so le trong)
Do đó: ∆ OED = ∆ OFB (g.c.g)
⇒ OE = OF
nên O là trung điểm của EF hay điểm E đối xứng với điểm F qua điểm O.
Câu 97: Cho hình 15 trong đó ABCD là hình bình hành. Chứng minh rằng các điểm H và K đối xứng với nhau qua điểm O.
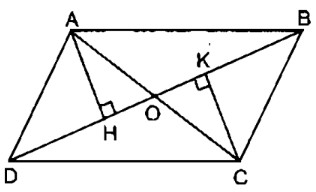
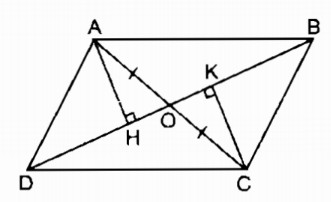
Xét hai tam giác vuông AHO và CKO:
\(\widehat {AHO} = \widehat {CKO} = {90^0}\)
OA = OC ( tính chất hình bình hành)
Advertisements (Quảng cáo)
\(\widehat {AOH} = \widehat {COK}\) (đối đỉnh)
Do đó: ∆ AHO = ∆ CKO (cạnh huyền, góc nhọn)
⇒ OH = OK
nên O là trung điểm của HK hay điểm H đối xứng với điểm K qua điểm O.
Câu 98: Cho tam giác ABC, D là trung điểm của AB, E là trung điểm của AC. Gọi O là một điểm bất kì nằm trong tam giác ABC. Vẽ điểm M đối xứng với O qua D, vẽ điểm N đối xứng với O qua E. Chứng minh rằng MNCB là hình bình hành.
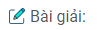
Xét tứ giác AOBM:
DA = DB (gt)
DO = DM (định nghĩa đối xứng tâm)
Suy ra: Tứ giác AOBM là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)
Advertisements (Quảng cáo)
⇒ BM // AO và BM = AO (1)
Xét tứ giác AOCN:
EA = EC (gt)
EO = EN (định nghĩa đối xứng tâm)
Suy ra: Tứ giác AOCN là hình bình hành ( vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)
⇒ CN // AO và CN = AO (2)
Từ (1) và (2) suy ra: BM // CN và BM = CN
Vậy : Tứ giác BMNC là hình bình hành ( vì có một cặp cạnh đối song song và bằng nhau)
Câu 99: Cho tam giác ABC, các đường trung tuyến AD, BE, CF cắt nhau ở G. Gọi H là điểm đối xứng với G qua D, I là điểm đối xứng với G qua E, K là điểm đối xứng với G qua F. Tìm các điểm đối xứng với A, với B, với C qua G.
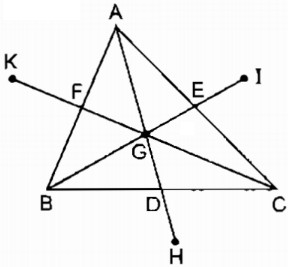
Ta có: GD = DH (tính chất đối xứng tâm)
⇒ GH = 2GD (1)
GA = 2GD ( tính chất đường trung tuyến của tam giác) (2)
Từ (1) và (2) suy ra: GA = GH
nên điểm đối xứng với điểm A qua tâm G là điểm H
GE = EI (tính chất đối xứng tâm)
⇒ GI = 2GE (3)
GB = 2GE (tính chất đường trung tuyến của tam giác) (4)
Từ (3) và (4) suy ra: GB = GI
nên điểm đối xứng với điểm B qua tâm G là điểm I
GF = FK (tính chất đối xứng tâm)
⇒ GK = 2GF (5)
GC = 2GF (tính chất đường trung tuyến của tam giác) (6)
Từ (5) và (6) suy ra: GC = GK
nên điểm đối xứng với điểm C qua tâm G là điểm K

