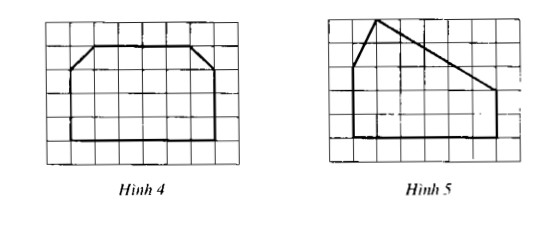
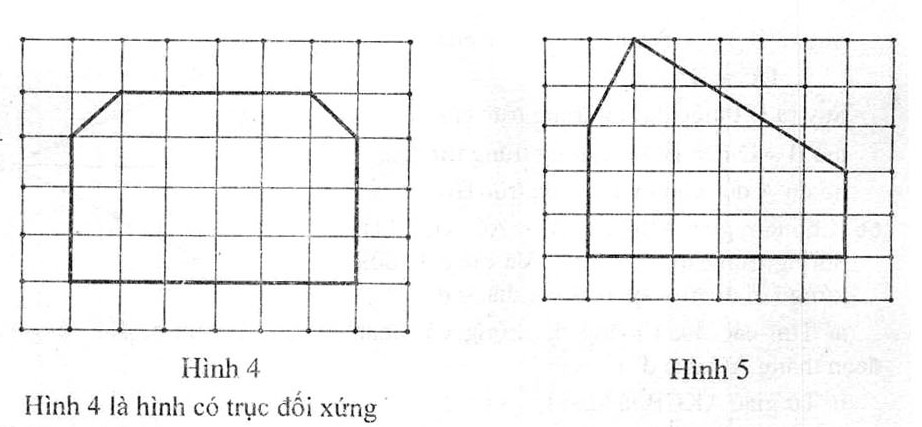
Câu 68: Trong các hình nét đậm vẽ trên giấy kẻ ô vuông ở hình 4, hình 5, hình nào có trục đối xứng ?
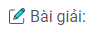
Câu 70: Điền dấu “x” vào ô thích hợp:
| Câu khẳng định | Đúng | Sai |
| a. Tam giác có một trục đối xứng là tam giác cân | ||
| b. Tam giác có một trục đối xứng là hình thang cân |
Giải
| Câu khẳng định | Đúng | Sai |
| a. Tam giác có một trục đối xứng là tam giác cân | x | |
| b. Tam giác có một trục đối xứng là hình thang cân | x |
Câu 71: Chứng minh rằng giao điểm hai đường chéo của hình thang cân nằm trên trục đối xứng của hình thang cân.
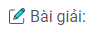
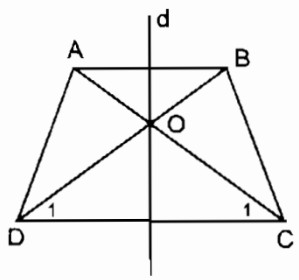
Hình thang cân ABCD có AB // CD. Gọi O là giao điểm của hai đường chéo AC và BD.
Xét ∆ ADC và ∆ BCD:
AD = BC ( tính chất hình thang cân)
AC = BD ( tính chất hình thang cân)
Advertisements (Quảng cáo)
CD cạnh chung
Do đó ∆ ADC = ∆ BCD (c.c.c)
\( \Rightarrow {\widehat D_1} = {\widehat C_1}\)
⇒ ∆ OCD cân tại O
⇒ OC = OD nên O nằm trên đường trung trực của CD.
Trục đối xứng của hình thang cân là đường thẳng trung trực của hai đáy.
Vậy O thuộc trục đối xứng của hình thang cân.
Câu 72: Cho góc nhọn xOy, điểm A nằm trong góc đó. Dựng điểm B thuộc tia Ox, điểm C thuộc tia Oy sao cho tam giác ABC có chu vi nhỏ nhất.
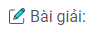
Advertisements (Quảng cáo)
Cách dựng:
– Dựng điểm D đối xứng với A qua Ox
– Dựng điểm E đối xứng với A qua tia Oy
– Nối DE cắt Ox tại B, Oy tại C
Tam giác ABC là tam giác có chu vi nhỏ nhất.
Vì \(\widehat {xOy} < {90^0}\) nên DE luôn cắt Ox và Oy do đó ∆ ABC luôn dựng được.
Chứng minh:
Chu vi ∆ ABC bằng AB + BC + AC
Vì D đối xứng với A qua Ox nên Õ là đường trung trực của AD
⇒ AB = BD ( tính chất đường trung trực)
E đối xứng với A qua Oy nên Oy là đường trung trực của AE
⇒AC = CE ( tính chất đường trung trực)
Suy ra: AB + BC + AC = BD + BC + CE = DE (1)
Lấy B’ bất kì trên Ox, C’ bất kì trên tia Oy. Nối C’E, C’A, B’A, B’D.
Ta có: B’A = B’D ( tính chất đường trung trực)
C’A = C’E (tính chất đường trung trực)
Chu vi ∆ AB’C’ bằng AB’ + AC’ + B’C’ = B’D + B’C’ +C’E (2)
Vì DE ≤ B’D + B’C’ + C’E (dấu bằng sảy ra khi B’ trùng B. C’ trùng C)
nên chu vi của ∆ ABC ≤ chu vị của ∆ A’B’C’
Vậy ∆ ABC có chu vi bé nhất.

