Câu 103: Trong các hình sau, hình nào có tâm đối xứng ? Với các hình đó, hãy chỉ rõ tâm đối xứng của hình.
a. Đoạn thẳng AB.
b. Tam giác đều ABC.
c. Đường tròn tâm O.

Hình có tâm đối xứng là:
a. Đoạn thẳng AB là hình có tâm đối xứng. Tâm đối xứng của đoạn thẳng AB là trung điểm của nó.
b. Tam giác đều ABC là hình không có tâm đối xứng
c. Đường tròn tâm O là hình có tâm đối xứng. Tâm đối xứng của (O) là tâm của đường tròn đó.
Câu 104: Cho góc xOy và điểm A nằm trong góc đó.
a. Vẽ điểm B đối xứng với O qua A. Qua B kẻ đường thẳng song song với Ox, cắt Oy ở C. Gọi D là giao điểm của CA và Ox. Chứng minh rằng các điểm C và D đối xứng với nhau qua điểm A.
b. Từ đó suy ra cách dựng đường thẳng đi qua A, cắt Ox, Oy ở D, C sao cho A là trung điểm của CD.

Advertisements (Quảng cáo)

a. Xét ∆ OAD và ∆ BAC:
OA = AB (tính chất đối xứng tâm)
\({\widehat A_1} = {\widehat A_2}\) (đối đỉnh)
\({\widehat O_1} = {\widehat B_1}\) (so le trong)
Do đó: ∆ OAD = ∆ BAC (g.c.g)
⇒ AD = AC
Suy ra: C đối xứng với D qua tâm A.
Advertisements (Quảng cáo)
b. Cách dựng :
– Dựng B đối xứng với O qua tâm A
– Qua B dựng đường thẳng song song Ox cắt Oy tại C.
– Dựng tia CA cắt Ox tại D.
Ta có D là điểm cần dựng.
Chứng minh : (như câu a)
Câu 105: Cho tam giác ABC, điểm M nằm trên cạnh BC. Gọi O là trung điểm của AM. Dựng điểm E thuộc cạnh AB, điểm F thuộc cạnh AC sao cho E đối xứng với F qua O

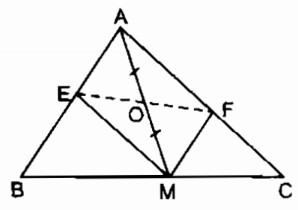
– Qua điểm M dựng đường thẳng song song với AC cắt AB tại E
– Qua điểm M dựng đường thẳng song song với AB cắt AC tại F
Ta có E, F là hai điểm cần dựng.
Chứng minh :
ME // AC hay ME // AF
MF // AB hay MF // AE
nên Tứ giác AEMF là hình bình hành (theo định nghĩa)
O là trung điểm của AM
Suy ra: EF đi qua O (tính chất hình bình hành)
⇒ OE = OF
Vậy E đối xứng với F qua tâm O.

