Câu 57: Dựng hình thang cân ABCD, biết hai đáy AB = 1cm, CD = 3cm, đường chéo BD = 3cm.
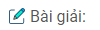
Phân tích: Giả sử hình thang ABCD dựng được thỏa mãn điều kiện bài toán.
Từ B kẻ đường thẳng song song với AC cắt CD tại E. Tứ giác ABEC là hình thang có hai cạnh bên song song nên CE = AB = 1cm, BE = AC = 3cm
Tam giác BDE xác định được, ta cần xác định đỉnh C và A
– Đỉnh C nằm trên tia DE cách D một khoảng bẳng 3cm
– Đỉnh A nằm trên đường thẳng đi qua B và song song với CD, A cách C một khoảng bằng 3cm
Cách dựng:
– Dựng ∆ BDE biết BD = 3cm, BE = 3cm, DE = 4cm.
– Dựng điểm C trên tia DE sao cho DC = 3cm
– Dựng đường thẳng d đi qua B song song với CD
Advertisements (Quảng cáo)
– Dựng cung tròn tâm C bán kính 3cm cắt đường thẳng d tại A.
Nối AD ta có hình thang ABCD dựng được.
Chứng minh: Thật vậy theo cách dựng ta có AB // CD.
Tứ giác ABCD là hình thang
CD = 3cm, AC = BD = 3cm. Vậy ABCD là hình thang cân
Thỏa mãn điều kiện bài toán.
Bài toán có một nghiệm hình.
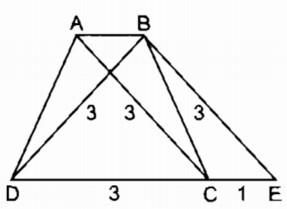
Câu 58: Dựng tứ giác ABCD, biết AB = 2cm, AD = 3cm, \(\widehat A = {80^0},\widehat B = {120^0},\widehat C = {100^0}\).
Advertisements (Quảng cáo)
Cách dựng:
– Dựng ∆ ABD biết AB = 2cm, \(\widehat A = {80^0}\), AD = 3cm.
– Dựng \(\widehat {ABx} = {120^0}\)
– Trên nửa mặt phẳng bờ AD chứa đỉnh D dựng \(\widehat {ADy} = {60^0}\). Dy cắt Bx tại C.
Chứng minh: Thật vậy theo cách dựng AB = 2cm, \(\widehat A = {80^0}\), AD = 3cm, \(\widehat B = {120^0}\)
\(\eqalign{
& \widehat C = {360^0} – \left( {\widehat A + \widehat B + \widehat D} \right) \cr
& = {360^0} – \left( {{{80}^0} + {{120}^0} + {{60}^0}} \right) = {100^0} \cr} \)
Tứ giác ABCD dựng được thỏa mãn điều kiện bài toán.
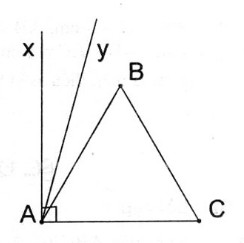
Câu 59: Dựng góc \({75^0}\) bằng thước và compa.
Cách dựng:
– Dựng tam giác ABC đều
– Trên nửa mặt phẳng bờ AC chứa điểm B dựng tia Ax ⊥ AC
– Dựng tia phân giác Ay của \(\widehat {xAB}\) ta có \(\widehat {CAy} = {75^0}\)
Chứng minh: thật vậy ∆ ABC đều nên \(\widehat {BAC} = {60^0},\widehat {xAC} = {90^0}\)
\(\eqalign{
& \Rightarrow \widehat {BAx} = \widehat {xAC} – \widehat {BAC} = {90^0} – {60^0} = {30^0} \cr
& \widehat {BAy} = {1 \over 2}\widehat {BAx} = {15^0} \cr
& \Rightarrow \widehat {CAy} = \widehat {BAC} + \widehat {BAy} = {60^0} + {15^0} = {75^0} \cr} \)

