Câu 30: Cho tam giác ABC cân tại A. Lấy điểm D trên cạnh AB, điểm E trên cạnh AC sao cho AD = AE.
a. Tứ giác BDEC là hình gì ? Vì sao ?
b. Các điểm D, E ở vị trí nào thì BD = DE = EC ?
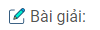
a. AD = AE (gt)
⇒ ∆ ADE cân tại A
\( \Rightarrow \widehat {ADE} = {{{{180}^0} – \widehat A} \over 2}\)
∆ ABC cân tại A
\( \Rightarrow \widehat {ABC} = {{{{180}^0} – \widehat A} \over 2}\)
Suy ra: \(\widehat {ADE} = \widehat {ABC}\)
⇒ DE // BC (vì có cặp góc đồng vị bằng nhau)
Tứ giác BDEC là hình thang
\(\widehat {ABC} = \widehat {ACB}\) (tính chất tam giác cân)
Hay \(\widehat {DBC} = \widehat {ECB}\). Vậy BDEC là hình thang cân
b. Ta có: BD = DE ⇒ ∆ BDE cân tại D
\( \Rightarrow {\widehat B_1} = {\widehat E_1}\)
Mà \({\widehat E_1} = {\widehat B_2}\) (so le trong)
\( \Rightarrow {\widehat B_1} = {\widehat B_2}\)
DE = EC ⇒∆ DEC cân tại E
\( \Rightarrow {\widehat D_1} = {\widehat C_1}\)
\({\widehat D_1} = {\widehat C_2}\) (so le trong)
\( \Rightarrow {\widehat C_1} = {\widehat C_2}\)
Vậy khi BE là tia phân giác của \(\widehat {ABC}\), CD là tia phân giác của \(\widehat {ACB}\) thì BD = DE = EC.
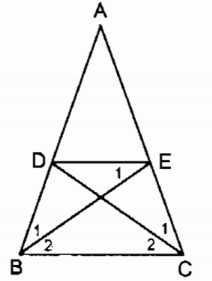
Câu 31: Hình thang cân ABCD có O là giao điểm của hai đường thẳng chứa cạnh bên AD, BC và E là giao điểm của hai đường chéo. Chứng minh rằng OE là đường trung trực của hai đáy.
\(\eqalign{
& \widehat {ADC} = \widehat {BCD}\,\,\,\,(gt) \cr
& \Rightarrow \widehat {ODC} = \widehat {OCD} \cr} \)
Advertisements (Quảng cáo)
⇒ ∆ OCD cân tại O
⇒ OC = OD
⇒ OA + AD = OB + BC
Mà AD = BC (tính chất hình thang cân)
⇒ OA = OB
Xét ∆ ADC và ∆ BCD :
AD = BC (chứng minh trên)
AC = BD (tính chất hình thang cân)
CD cạnh chung
Do đó: ∆ ADC = ∆ BCD (c.c.c)
\( \Rightarrow {\widehat D_1} = {\widehat C_1}\)
⇒ ∆ EDC cân tại E
⇒ EC = ED nên E thuộc đường trung trực của CD
OC = OD nên O thuộc đường trung trực của CD
E≢ O. Vậy OE là đường trung trực của CD.
BD = AC (chứng minh trên)
⇒ EB + ED = EA + EC mà ED = EC
⇒ EB = EA nên E thuộc đường trung trực AB
Advertisements (Quảng cáo)
E≢ O. Vậy OE là đường trung trực của AB.
Câu 32: a. Hình thang cân ABCD có đáy nhỏ AB = b, đáy lớn CD = a, đường cao AH.
Chứng minh rằng (a và b có cùng đơn vị đo)
b. Tính đường cao của hình thang cân có hai đáy 10cm, 26cm và cạnh bên 17cm
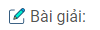
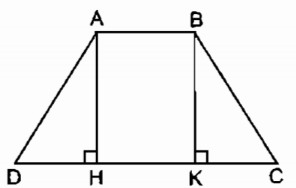
a. Kẻ đường cao BK
Xét hai tam giác vuông AHD và BKC, ta có:
\(\widehat {AHB} = \widehat {BKC} = {90^0}\)
AD = BC (tính chất hình thang cân)
\(\widehat D = \widehat C\) (gt)
Do đó: ∆ AHD = ∆ BKC (cạnh huyền, góc nhọn)
⇒ HD = KC
Hình thang ABKH có hai cạnh bên song song nên AB = HK
a−b = DC – AB = DC – HK = HD + KC = 2HD
\( \Rightarrow HD = {{a – b} \over 2}\)
\(HD = DC-HD = a – {{a – b} \over 2} = {{a + b} \over 2}\)
b. \(HD = {{CD – AB} \over 2} = {{26 – 10} \over 2} = 8\left( {cm} \right)\)
Trong tam giác vuông AHD có \(\widehat {AHD} = {90^0}\)
\(A{D^2} = A{H^2} + H{D^2}\) (định lí Pi-ta-go)
\(\eqalign{
& \Rightarrow A{H^2} = A{D^2} – H{D^2} \cr
& A{H^2} = {17^2} – {8^2} = 289 – 64 = 225 \cr
& AH = 15(cm) \cr} \)
Câu 33: Hình thang cân ABCD có đường chéo DB vuông góc với cạnh bên BC, BD là tia phân giác của góc D. Tính chu vi của hình thang, biết BC = 3cm.
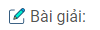
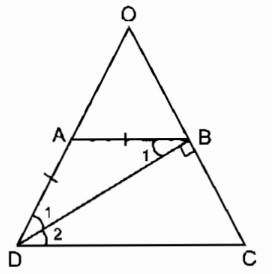
Ta có: AD = BC = 3 (cm) (tính chất hình thang cân)
\(\widehat {ABD} = \widehat {BDC}\) (so le trong)
\(\eqalign{
& \widehat {ADB} = \widehat {BDC}(gt) \cr
& \Rightarrow \widehat {ABD} = \widehat {ADB} \cr} \)
⇒ ∆ ABD cân tại A
⇒ AB = AD = 3 (cm)
∆ BDC vuông tại B
\( \Rightarrow \widehat {BDC} + \widehat C = {90^0}\)
\(\widehat {ADC} = \widehat C\) (gt)
Mà \(\widehat {BDC} = {1 \over 2}\widehat {ADC}\) nên \(\widehat {BDC} = {1 \over 2}\widehat C\)
\(\widehat C + {1 \over 2}\widehat C = {90^0} \Rightarrow \widehat C = {60^0}\)
Từ B kẻ đường thẳng song song AD cắt CD tại E.
Hình thang ABED có hai cạnh bên song song nên AB = DE và AD = BE
⇒ DE = 3 (cm), BE = 3 (cm)
\(\widehat {BEC} = \widehat {ADC}\) (đồng vị )
Suy ra: \(\widehat {BEC} = \widehat C\)
⇒ ∆ BEC cân tại B có \(\widehat C = {60^0}\)
⇒ ∆ BEC đều
⇒ EC = BC = 3 (cm)
CD = CE + ED = 3 + 3 = 6 (cm)
Chu vi hình thang ABCD bằng:
AB + BC + CD + DA = 3+3 +6 +3=15 (cm)

