Câu 15: Chứng minh rằng trong hình thang có nhiều nhất là hai góc tù, có nhiều nhất là hai góc nhọn
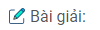
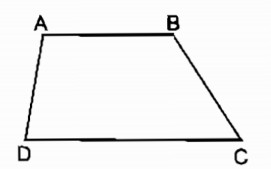
Xét hình thang ABCD có AB// CD
\(\widehat A\) và \(\widehat D\) là hai góc kề với cạnh bên.
\( \Rightarrow \widehat A + \widehat D = {180^0}\) (2 góc trong cùng phía ) nên trong hai góc đó có nhiều nhất 1 góc nhọn và có nhiều nhất là 1 góc tù.
\(\widehat B\) và \(\widehat C\) là hai góc kề với cạnh bên
\( \Rightarrow \widehat B + \widehat C = {180^0}\) (2 góc trong cùng phía) nên trong hai góc đó có nhiều nhất 1 góc nhọn và có nhiều nhất 1 góc tù. Vậy bốn góc là : \(\widehat A,\widehat B,\widehat C,\widehat D\) có nhiều nhất là hai góc nhọn và nhiều nhất là hai góc tù.
Câu 16: Chứng minh rằng trong hình thang các tia phân giác của hai góc kề một cạnh bên vuông góc với nhau.
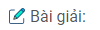
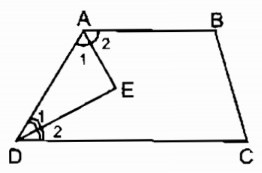
Giải sử hình thang ABCD có AB// CD
Advertisements (Quảng cáo)
\(\eqalign{
& {\widehat A_1} = {\widehat A_2} = {1 \over 2}\widehat A(gt) \cr
& {\widehat D_1} = {\widehat D_2} = {1 \over 2}\widehat D(gt) \cr} \)
Mà \(\widehat A + \widehat D = {180^0}\) (hai góc trong cùng phía bù nhau)
Suy ra:
\({\widehat A_1} + {\widehat D_1} = {1 \over 2}\widehat A + \widehat D = {90^0}\)
Trong ∆ AED ta có :
\(\widehat {AED} + {\widehat A_1} + {\widehat D_1} = {180^0}\) (tổng ba góc trong tam giác)
\( \Rightarrow \widehat {AED} = {180^0} – \left( {{{\widehat A}_1} + {{\widehat D}_1}} \right) = {180^0} – {90^0} = {90^0}\)
Vậy AE ⊥ DE
Advertisements (Quảng cáo)
Câu 17: Cho tam giác ABC . Các tia phân giác của các góc B và C cắt nhau ở I. Qua I kẻ đường thẳng song song với BC, cắt các cạnh AB và AC ở D và E.
a. Tìm các hình thang trong hình vẽ
b. Chứng minh rằng hình thang BDEC có một cạnh đáy bằng tổng hai cạnh bên.
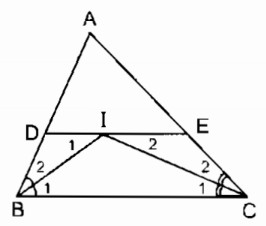
a. Đường thẳng đi qua I song song với BC cắt AB tại D và AC tại E, ta có các hình thang sau: BDEC, BDIC, BIEC.
b. DE // BC (theo cách vẽ)
\( \Rightarrow {\widehat I_1} = {\widehat B_1}\) (hai góc so le trong)
Mà \({\widehat B_1} = {\widehat B_2}\) (gt)
Suy ra: \({\widehat I_1} = {\widehat B_2}\)
Do đó: ∆ BDI cân tại D
⇒ DI = DB (1)
Ta có: \({\widehat I_2} = {\widehat C_1}\) (so le trong)
\({\widehat C_1} = {\widehat C_2}\) (gt)
Suy ra: \({\widehat I_2} = {\widehat C_2}\) do đó: ∆ CEI cân tại E
⇒ IE = EC (2)
DE = DI + IE (3)
Từ (1), (2) và (3) suy ra: DE = BD + CE

