Câu 1: Tính tổng các góc ngoài của tứ giác (tại mỗi đỉnh của tứ giác chỉ chọn một góc ngoài).
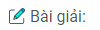
Ta có:
\({\widehat A_1} + {\widehat B_1} + {\widehat C_1} + {\widehat D_1} = {360^0}\) (tổng các góc của tứ giác)
Tại mỗi đỉnh của tứ giác tổng một góc trong và một góc ngoài bằng 180°
nên
\(\eqalign{
& {\widehat A_1} + {\widehat A_2} + {\widehat B_1} + {\widehat B_2} + {\widehat C_1} + {\widehat C_2} + {\widehat D_1} + {\widehat D_2} \cr
& = {180^0}.4 = {720^0} \cr
& \Rightarrow {\widehat A_2} + {\widehat B_2} + {\widehat C_2} + {\widehat D_2} \cr
& = {720^0} – \left( {{{\widehat A}_1} + {{\widehat B}_1} + {{\widehat C}_1} + {{\widehat D}_1}} \right) \cr
& = {720^0} – {360^0} = {360^0} \cr} \)
Câu 2: Tứ giác ABCD có AB=BC, CD=DA.
a. Chứng minh rằng BD là đường trung trực của AC
Advertisements (Quảng cáo)
b. Cho biết \(\widehat B = {100^0},\widehat D = {70^0}\) tính \(\widehat A\) và \(\widehat C\).
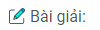
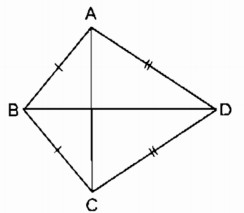
a) BA=BC (gt)
⇒ điểm B thuộc đường trung trực của AC
DA=DC (gt)
Advertisements (Quảng cáo)
⇒ điểm D thuộc đường trung trực của AC
B và D là hai điểm phân biệt cùng thuộc đường trung trực của AC nên đường thẳng BD là đường trung trực của AC.
b) Xét ∆ BAD và ∆ BCD, ta có:
BA = BC (gt)
DA = DC (gt)
BD cạnh chung
Do đó ∆ BAD =∆ BCD (c.c.c) \(\Rightarrow \widehat {BAD} = \widehat {BCD}\)
\(\eqalign{
& \widehat {BAD} + \widehat {BCD} + \widehat {ABC} + \widehat {ADC} = {360^0} \cr
& \widehat {BAD} + \widehat {BAD} = {360^0} – \left( {\widehat {ABC} + \widehat {ADC}} \right) \cr
& 2\widehat {BAD} = {360^0} – \left( {{{100}^0} + {{70}^0}} \right) = {190^0} \cr
& \Rightarrow \widehat {BAD} = {190^0}:2 = {95^0} \cr
& \Rightarrow \widehat {BCD} = \widehat {BAD} = {95^0} \cr} \)
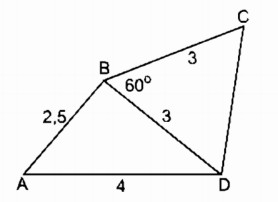
Câu 3: Vẽ lại tứ giác ABCD ở hình 1 vào vở bằng cách vẽ hai tam giác.
Vẽ ∆ABD, biết ba cạnh:
AD = 4cm, BD = 3cm, AB = 2.5 cm.
Vẽ ∆BCD, biết hai cạnh và góc xen giữa:
BD = 3cm, \(\widehat {DBC} = {60^0}\) , BC = 3cm (A và C thuộc hai nửa mặt phẳng đối nhau bờ BD)