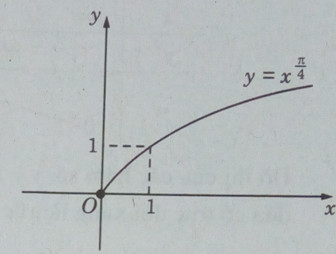Bài 2.6: Tìm tập xác định của các hàm số sau:
a) \(y = {({x^2} – 4x + 3)^{ – 2}}\)
b) \(y = {({x^3} – 8)^{{\pi \over 3}}}\)
c) \(y = {({x^3} – 3{x^2} + 2x)^{{1 \over 4}}}\)
d) \(y = {({x^2} + x – 6)^{ – {1 \over 3}}}\)
a) Hàm số xác định khi \({x^2} – 4x + 3 \ne 0\) hay \(x \ne 1;x \ne 3\).
Vậy tập xác định của hàm số đã cho là R\{1; 3}.
b) Hàm số xác định khi x3 – 8 > 0 hay x > 2. Vậy tập xác định là \((2; + \infty )\) .
c) Hàm số xác định khi x3 – 3x2 + 2x > 0 hay x(x – 1)(x – 2) > 0
Suy ra 0 < x < 1 hoặc x > 2. Vậy tập xác định là \((0;1) \cup (2; + \infty )\)
d) Hàm số xác định khi x2 + x – 6 > 0 hay x < -3 và x > 2.
Vậy tập xác định là \(( – \infty ; – 3) \cup (2; + \infty )\).
Bài 2.7: Tính đạo hàm của các hàm số cho ở bài 2.6
a) \(y = {({x^2} – 4x + 3)^{ – 2}}\)
b) \(y = {({x^3} – 8)^{{\pi \over 3}}}\)
Advertisements (Quảng cáo)
c) \(y = {({x^3} – 3{x^2} + 2x)^{{1 \over 4}}}\)
d) \(y = {({x^2} + x – 6)^{ – {1 \over 3}}}\)
a) \(y’ = – 2{({x^2} – 4x + 3)^{ – 3}}(2x – 4)\)
b) \(y’ = {\pi \over 3}{({x^3} – 8)^{{\pi \over 3} – 1}}.3{x^2} = \pi {x^2}{({x^3} – 8)^{{\pi \over 3} – 1}}\)
c) \(y’ = {1 \over 4}{({x^3} – 3{x^2} + 2x)^{ – {3 \over 4}}}(3{x^2} – 6x + 2)\)
d) \(y’ = – {1 \over 3}{({x^2} + x – 6)^{ – {4 \over 3}}}(2x + 1)\).
Bài 2.8: Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
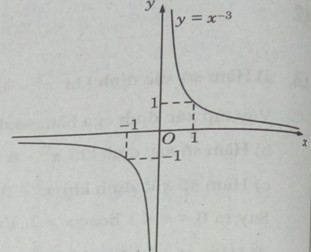
a) \(y = {x^{ – 3}}\)
b) \(y = {x^{ – {1 \over 2}}}\)
Advertisements (Quảng cáo)
c) \(y = {x^{{\pi \over 4}}}\)
a) Tập xác định: R\{0}
Hàm số đã cho là hàm số lẻ.
\(y’ = – 3{x^{ – 4}} = – {3 \over {{x^4}}}\)
Ta có: \(y’ < 0,\forall x \in R\backslash {\rm{\{ }}0\}\) nên hàm số luôn nghịch biến trên các khoảng xác định.
\(\mathop {\lim }\limits_{x \to – \infty } y = \mathop {\lim }\limits_{x \to + \infty } y = 0,\mathop {\lim }\limits_{x \to {0^ + }} y = + \infty ,\mathop {\lim }\limits_{x \to {0^ – }} y = – \infty \)
Đồ thị có tiệm cận ngang là trục hoành, tiệm cận đứng là trục tung.
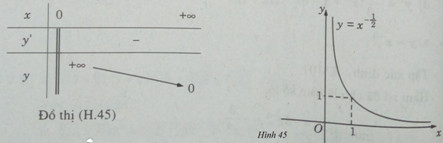
Bảng biến thiên:
Đồ thị của hàm số có tâm đối xứng là gốc tọa độ.
b) Tập xác định: \(D = (0; + \infty )\)
\(y’ = – {1 \over 2}{x^{ – {3 \over 2}}}\)
Vì nên hàm số nghịch biến.
\(\mathop {\lim }\limits_{x \to {0^ + }} y = + \infty ,\mathop {\lim }\limits_{x \to + \infty } y = 0\)
Đồ thị có tiệm cận đứng là trục tung, tiệm cận ngang là trục hoành.
Bảng biến thiên:
c) Tập xác định: \(D = (0; + \infty )\)
\(y’ > 0,\forall x \in D\)
Vì \(y’ > 0,\forall x \in D\) nên hàm số nghịch biến.
\(\mathop {\lim }\limits_{x \to {0^ + }} y = 0,\mathop {\lim }\limits_{x \to + \infty } y = + \infty \)
Đồ thị không có tiệm cận.
Bảng biến thiên
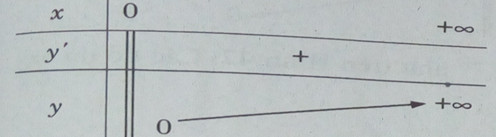Đồ thị
