Bài 40: a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số
\(y = {x^3} + 3{x^2} – 4\)
b) Viết phương trình tiếp tuyến của đồ thị tại điểm uốn.
c) Chứng minh rằng điểm uốn là tâm đối xứng của đồ thị.
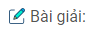
a) Tập xác đinh: \(D=\mathbb R\)
Sự biến thiên:
\(\eqalign{
& y’ = 3{x^2} + 6x \cr
& y’ = 0 \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr
x = – 2 \hfill \cr} \right. \cr} \)
– Hàm số đồng biến trên khoảng \(\left( { – \infty ; – 2} \right)\) và \(\left( {0; + \infty } \right)\)
– Hàm số nghịch biến trên khoảng \((-2;0)\)
– Cực trị:
Hàm số đạt cực đại tại \(x=-2\;;y_{CĐ}=0\)
Hàm số đạt cực tiểu tại \(x=0\;;y_{CT}=-4\)
– Giới hạn:
\(\eqalign{
& \mathop {\lim }\limits_{x \to + \infty } \left( {{x^3} + 3{x^2} – 4} \right) = + \infty \cr
& \mathop {\lim }\limits_{x \to – \infty } \left( {{x^3} + 3{x^2} – 4} \right) = – \infty \cr} \)
\(\eqalign{
& y” = 6x + 6 \cr
& y” = 0 \Leftrightarrow x = – 1 \cr} \)
Điểm uốn \(I(-1;-2)\)
– Bảng biến thiên:
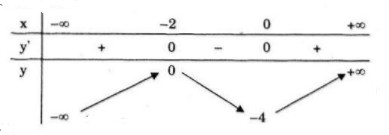
Đồ thị:
Đồ thị hàm số nhận điiểm \(I(-1;-2)\) làm tâm đối xứng.
b) \(y'(-1)=-3\)
Phương trình tiếp tuyến với đồ thị tại \(I(-1;-2)\) là:
\(y=-3(x+1)+(-2) \Leftrightarrow y = – 3x – 5\)
c) Đồ thị nhận \(I(-1;-2)\) làm tâm đối xứng khi và chỉ khi:
\(\eqalign{
& y\left( { – 1 + x} \right) + y\left( { – 1 – x} \right) = 2.\left( { – 2} \right) \cr
& \Leftrightarrow {\left( { – 1 + x} \right)^3} + 3{\left( { – 1 + x} \right)^2} – 4 + {\left( { – 1 – x} \right)^3} \cr&\;\;\;+ 3{\left( { – 1 – x} \right)^2} – 4 = – 4 \cr
& \Leftrightarrow – 1 + 3x – 3{x^2} + {x^3} + 3 – 6x + 3{x^2} – 4 – 1 \cr&\;\;\;- 3x – 3{x^2} – {x^3} + 3 + 6x + 3{x^2} – 4 = – 4 \cr
& \Leftrightarrow – 4 = – 4\,\,\forall x \cr} \)
\(\Leftrightarrow I(-1;-2)\) là tâm đối xứng của đồ thị.
Bài 41: a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số: \(y = – {x^3} + 3{x^2} – 1\).
b) Tùy theo các giá trị của \(m\), hãy biện luận số nghiệm của phương trình: \( – {x^3} + 3{x^2} – 1 = m\)
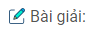
a) TXĐ: \(D =\mathbb R\)
Advertisements (Quảng cáo)
\(\eqalign{
& \mathop {\lim }\limits_{x \to + \infty } y = – \infty ;\,\mathop {\lim }\limits_{x \to – \infty } y = + \infty \cr
& y’ = – 3{x^2} + 6x = – 3x\left( {x – 2} \right);\cr&y’ = 0 \Leftrightarrow \left[ \matrix{
x = 0;\,y\left( 0 \right) = – 1 \hfill \cr
x = 2;\,y\left( 2 \right) = 3 \hfill \cr} \right. \cr} \)
Bảng biến thiên:
Hàm đồng biến trên khoảng \((0;2)\), nghịch biến trên mỗi khoảng \(\left( { – \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\).
Hàm số đạt cực tiểu tại điểm \(x = 0\), giá trị cực tiểu \(y(0) = -1\). Hàm số đạt cực đại tại điểm \(x = 2\), giá trị cực đại \(y(2) = 3\).
Đồ thị: \(y” = – 6x + 6;\,\,y” = 0 \Leftrightarrow x = 1;\,y\left( 1 \right) = 1\)
Xét dấu y”:

\(I(1;1)\) là điểm uốn của đồ thị
Điểm đặc biệt:
\(x = 0 \Rightarrow y = – 1\)
\(x = – 1 \Rightarrow y = 3\)
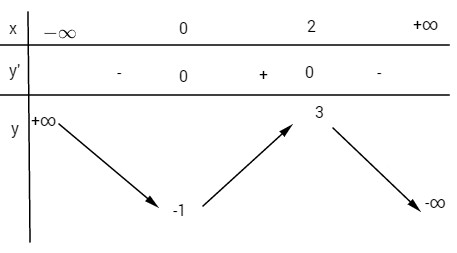
b) Số nghiệm của phương trình chính là số giao điểm của đồ thị \((C)\) hàm số \(y = – {x^3} + 3{x^2} – 1\) với đường thẳng \(y = m\) cùng phương với trục \(Ox\).
Dựa vào đồ thị ta có kết quả sau:
– Nếu \(m < -1\) hoặc \(m > 3\) thì phương trình có \(1\) nghiệm;
– Nếu \(m = -1\) hoặc \(m = 3\) thì phương trình có \(2\) nghiệm;
– Nếu \(-1 < m < 3\) thì phương trình có \(3\) nghiệm.
Bài 42: Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
a)\(y = {1 \over 3}{x^3} – {x^2} – 3x – {5 \over 3}\)
Advertisements (Quảng cáo)
b) \(y = {x^3} – 3x + 1\)
c) \(y = – {1 \over 3}{x^3} + {x^2} – 2x – {2 \over 3}\)
d) \(y = {x^3} – 3{x^2} + 3x + 1\)
Gỉải
a) TXĐ: \(D =\mathbb R\)
\(\eqalign{
& \mathop {\lim }\limits_{x \to + \infty } y = + \infty ;\,\,\mathop {\lim }\limits_{x \to – \infty } y = – \infty \cr
& y’ = {x^2} – 2x – 3;\cr&y’ = 0 \Leftrightarrow \left[ \matrix{
x = – 1 \hfill \cr
x = 3 \hfill \cr} \right.;\cr&y\left( { – 1} \right) = 0;\,\,y\left( 3 \right) = {{ – 32} \over 3} \cr} \)
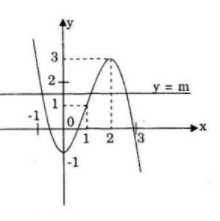
Bảng biến thiên:
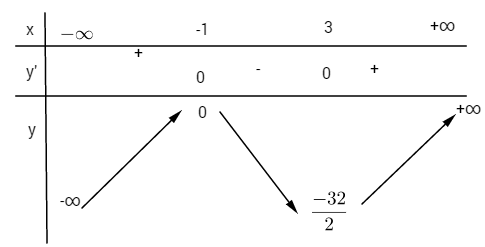
\(y” = 2x – 2;\,y” = 0 \Leftrightarrow x = 1;\,y\left( 1 \right) = – {{16} \over 3}\)
Xét dấu y”
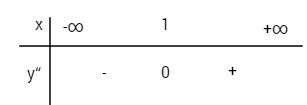
Điểm uốn \(I\left( {1; – {{16} \over 3}} \right)\)
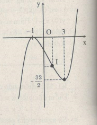
Điểm đặc biệt: \(x = 0 \Rightarrow y = {{ – 5} \over 3}\)
Đồ thị: Đồ thị nhận \(I\left( {1; – {{16} \over 3}} \right)\) làm tâm đối xứng.
b) TXĐ: \(D =\mathbb R\)
\(\eqalign{
& \mathop {\lim }\limits_{x \to + \infty } y = + \infty ;\,\mathop {\lim }\limits_{x \to – \infty } y = – \infty \cr
& y’ = 3{x^2} – 3;\,y’ = 0 \Leftrightarrow \left[ \matrix{
x = – 1 \hfill \cr
x = 1 \hfill \cr} \right.;\cr&,y\left( { – 1} \right) = 3;\,y\left( 1 \right) = – 1 \cr} \)
Bảng biến thiên:

\(y” = 6x;\,y” = 0 \Leftrightarrow x = 0;\,y\left( 0 \right) = 1\)
Xét dấu \(y”\)
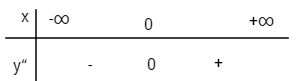
Điểm uốn \(I(0;1)\)
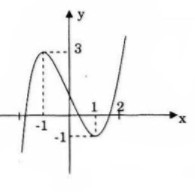
Điểm đặc biệt:\(x = 2 \Rightarrow y = 3\)
Đồ thị: Đồ thị nhận \(I(0;1)\) làm tâm đối xứng.
c) TXĐ: \(D =\mathbb R\)
\(\mathop {\lim }\limits_{x \to + \infty } y = – \infty ;\,\,\mathop {\lim }\limits_{x \to – \infty } y = + \infty \)
\(y’ = – {x^2} + 2x – 2 < 0\) với mọi \(x \in\mathbb R\)
Hàm số nghịch biến trên \(\mathbb R\)
Bảng biến thiên:
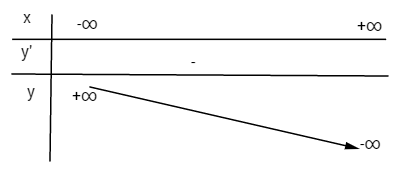
\(y” = – 2x + 2;\,y” = 0 \Leftrightarrow x = 1;\,y\left( 1 \right) = – 2\)
Xét dấu \(y”\)
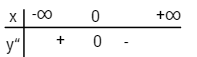
Điểm uốn \(I(1;-2)\)
Điểm đặc biết:\(x = 0 \Rightarrow y = {{ – 2} \over 3}\)
Đồ thị: Đồ thị nhận \(I(1;-2)\) làm tâm đối xứng.
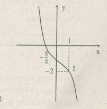
d) TXĐ: \(D =\mathbb R\)
\(\mathop {\lim }\limits_{x \to + \infty } y = + \infty ;\,\mathop {\lim }\limits_{x \to – \infty } y = – \infty \)
\(y’ = 3{x^2} – 6x + 3 = 3{\left( {x – 1} \right)^2} \ge 0\) với mọi \(x \in\mathbb R\)
Dấu bằng chỉ xảy ra khi \(x = 1\)
Hàm số đồng biến trên \(\mathbb R\)
Bảng biến thiên:
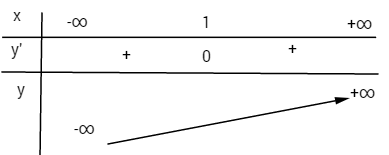
Xét dấu \(y”\)
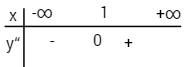
Điểm uốn \(I(1;2)\)
Điểm đặc biệt: \(x = 0 \Rightarrow y = 1\)
Đồ thị: Đồ thị nhận \(I(1;2)\) làm tâm đối xứng.