Câu 4.1: Tính diện tích của hình được cho trong mỗi trường hợp sau:
a. Hình thang ABCD, đáy lớn AB = 10cm, đáy nhỏ CD = 6cm và đường cao DE = 5cm.
b. Hình thang cân ABCD, đáy nhỏ CD = 6cm, đường cao DH = 4cm và cạnh bên AD = 5cm.
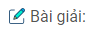
a. Áp dụng công thức tính diện tích hình thang.
\(S = {{a + b} \over 2}.h = {{10 + 6} \over 2}.5 = 40(c{m^2})\)
b. Xét hình thang cân ABCD có AB // CD
Đáy nhỏ CD = 6cm, cạnh bên AD = 5cm
Đường cao DH = 4cm. Kẻ CK ⊥ AB
Ta có tứ giác CDHK là hình chữ nhật
HK = CD = 6cm
∆ AHD vuông tại H. Theo định lý Pi-ta-go ta có: \(A{D^2} = A{H^2} + D{H^2}\)
\( \Rightarrow {\rm A}{{\rm H}^2} = A{D^2} – D{H^2} = {5^2} – {4^2} = 25 – 16 = 9 \Rightarrow AH = 3cm\)
Xét hai tam giác vuông DHA và CKB :
\(\widehat {DHA} = \widehat {CKB} = 90^\circ \)
AD = BC (tính chất hình thang cân)
\(\widehat A = \widehat B\) (gt)
Do đó: ∆ DHA = ∆ CKB (cạnh huyền, góc nhọn)
Advertisements (Quảng cáo)
⇒ KB = AH = 3 (cm)
AB = AH + HK + KB = 3+ 6+ 3 = 12 (cm)
\({S_{ABCD}} = {{AB + CD} \over 2}.DH = {{12 + 6} \over 2}.4 = 36(c{m^2})\)
Câu 4.2: Cho hình thang ABCD có đáy nhỏ CD và đáy lớn AB
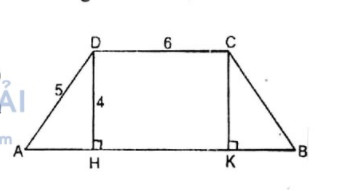
a. Hãy vé tam giác ADE mà diện tích của nó bằng diện tích hình thang đã cho. Từ đó suy ra cách tính diện tích hình thang dựa vào độ dài hai cạnh đáy và độ dài đường cao của hình thang.
b. Hãy chia hình thang đã cho thành hai phần có diện tích bằng nhau bằng một đường thẳng đi qua đỉnh D của nó.
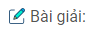
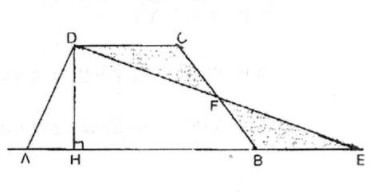
a. Gọi F là trung điểm của cạnh bên BC. Cắt hình thang theo đường DF đưa ghép về như hình vẽ bên, điểm C trung với điểm B, D trùng với E.
Vì AB // CD \( \Rightarrow \widehat {ABC} + 180^\circ \Rightarrow {\rm A},{\rm B},{\rm E}\) thẳng hàng
\(\widehat {ABF} + \widehat {DFC} = 180^\circ \)
⇒ D, F, E thẳng hàng
Advertisements (Quảng cáo)
∆ DFC = ∆ EFB (g.c.g)
\({S_{DFC}} = {S_{EFB}}\)
Suy ra: \({S_{ABCD}} = {S_{ADE}}\)
∆ DFC = ∆ EFB⇒ DC = BE
AE = AB + BE = AB + DC
\({S_{ADE}} = {1 \over 2}DH.AE = {1 \over 2}DH.\left( {AB + CD} \right)\)
Vậy : \({S_{ABCD}} = {1 \over 2}DH.\left( {AB + CD} \right)\)
b. Dựa trên hình vẽ câu a ta chọn điểm K là trung điểm AE.
Ta nối DK cắt hình thang theo đường DK ta có hai phần diện tích bằng nhau:
Một phần là ∆ ADK có \(AK = {{AB + CD} \over 2}\)
Một phần là hình thang BCDK có hai đáy CD + BK = \({{AB + CD} \over 2}\)
Và có chiều cao bằng nhau nên có diện tích bằng nhau.
Câu 4.3: Cho hình bình hành ABCD có diện tích S. Trên cạnh BC lấy hai điểm M, N sao cho BM = MN = NC = \({1 \over 3}\)BC
a. Tính diện tích của tứ giác ABMD theo S
b. Từ điểm N kẻ NT song song với AB (T thuộc AC). Tính diện tích của tứ giác ABNT theo S
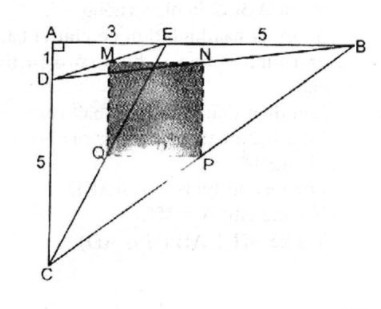
a. ∆ DMC có CM = \({2 \over 3}\)BC
Hình bình hành ABCD và ∆ DMC có chung đường cao kẻ từ đỉnh D đến BC.
Gọi độ dài đường cao là h, BC = a
Ta có diện tích hình bình hành ABCD là S = a h
\(\eqalign{ & {S_{DMC}} = {1 \over 2}h.{2 \over 3}a = {1 \over 3}ah = {1 \over 3}S \cr & {S_{ABMD}} = {S_{ABCD}} – {S_{DMC}} = S – {1 \over 3}S = {2 \over 3}S \cr} \)
b. \({S_{ABC}} = {1 \over 2}{S_{ABCD}} = {S \over 2}\)
\(CN = {1 \over 3}BC\), NT // AB.
Theo tính chất đường thẳng song song cách đều \( \Rightarrow CT = {1 \over 3}AC\)
∆ ABC và ∆ BTC có chung chiều cao kẻ từ đỉnh B, đáy \(CT = {1 \over 3}AC\)
\( \Rightarrow {S_{BTC}} = {1 \over 3}{S_{ABC}} = {1 \over 3}.{S \over 2} = {S \over 6}\)
∆ BTC và ∆ TNC có chung chiều cao kẻ từ đỉnh T, cạnh đáy $CN = {1 \over 3}CB$
\(\eqalign{ & \Rightarrow {S_{TNC}} = {1 \over 3}{S_{BTC}} = {1 \over 3}.{S \over 6} = {S \over {18}} \cr & \Rightarrow {S_{ABNT}} = {S_{ABC}} – {S_{TNC}} = {S \over 2} – {S \over {18}} = {{9S} \over {18}} – {S \over {18}} = {{4S} \over 9} \cr} \)

