Bài 1: Trong không gian \(Oxyz\) cho ba vectơ
\(\overrightarrow a = ( – 1;1;0)\), \(\overrightarrow b = (1;1;0)\) và \(\overrightarrow c = (1;1;1)\)
Trong các mệnh đề sau, mệnh đề nào sai?
(A) \(\left| {\overrightarrow a } \right| = \sqrt 2 \); (B) \(\left| {\overrightarrow c } \right| = \sqrt 3 \);
(C) \(\overrightarrow a \bot \overrightarrow b \); (D) \(\overrightarrow b \bot \overrightarrow c \).
Chọn (D) \(\overrightarrow b \bot \overrightarrow c \).
Bài 2: Trong không gian \(Oxyz\) cho ba vectơ
\(\overrightarrow a = ( – 1;1;0)\), \(\overrightarrow b = (1;1;0)\) và \(\overrightarrow c = (1;1;1)\).
Trong các mệnh đề sau, mệnh đề nào đúng?
(A) \(\overrightarrow a .\overrightarrow c = 1;\)
(B) \(\overrightarrow a ,\overrightarrow b \) cùng phương;
(C) cos (\(\overrightarrow b \), \(\overrightarrow c \))= \({2 \over {\sqrt 6 }}\);
(D) \(\overrightarrow a \) + \(\overrightarrow b \) + \(\overrightarrow c \) = \(\overrightarrow 0 \)
Chọn (C) cos (\(\overrightarrow b \), \(\overrightarrow c \))= \({2 \over {\sqrt 6 }}\)
Bài 3: Trong không gian \(Oxyz\) cho ba vectơ
\(\overrightarrow a = ( – 1;1;0)\), \(\overrightarrow b = (1;1;0)\) và \(\overrightarrow c = (1;1;1)\)
Cho hình bình hành \(OADB\) có \(\overrightarrow {OA} \) = \(\overrightarrow a \), \(\overrightarrow {OB} = \overrightarrow b \) (\(O\) là gốc toạ độ). Toạ độ của tâm hình bình hành \(OADB\) là:
(A) \((0 ; 1 ; 0)\) (B) \((1 ; 0 ; 0)\)
(C) \((1 ; 0 ; 1)\) (D) \((1 ; 1 ; 0)\).
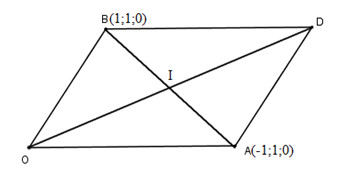
Gọi tọa độ của \(D(x;y;z)\)
\(OADB\) là hình bình hành nên \(\overrightarrow {OD} = \overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow a + \overrightarrow b=(0;2;0) \)
Gọi \(I\) là tâm của hình bình hành nên \(\vec{OI}={1\over2}\vec{OD}=(0;1;0)\)
Vậy \(I(0;1;0)\)
Chọn (A) \((0 ; 1 ; 0)\).
Bài 4: Trong không gian \(Oxyz\) cho bốn điểm \(A(1; 0; 0), B(0; 1; 0), C(0; 0; 1)\) và \(D(1; 1; 1)\)
Trong các mệnh đề sau, mệnh đề nào sai?
(A) Bốn điểm A, B, C, D tạo thành một tứ diện ;
(B) Tam giác ABD là tam giác đều ;
(C) \(AB ⊥ CD\) ;
(D) Tam giác \(BCD\) là tam giác vuông.
Ta có:
\(\eqalign{
& \overrightarrow {AB} = ( – 1;1;0) \cr
& \overrightarrow {CD} = (1;1;0) \cr
& \overrightarrow {AB} .\overrightarrow {CD} = – 1.1 + 1.1 + 0.0 = 0 \cr} \)
Chọn (D) Tam giác \(BCD\) là tam giác vuông.
Bài 5: Trong không gian \(Oxyz\) cho bốn điểm \(A(1; 0; 0), B(0; 1; 0), C(0; 0; 1)\) và \(D(1; 1; 1)\)
Gọi \(M, N\) lần lượt là trung điểm của \(AB\) và \(CD\). Toạ độ điểm \(G\) là trung điểm của \(MN\) là:
(A) G \(\left( {{1 \over 3};{1 \over 3};{1 \over 3}} \right)\) ; (B) G \(\left( {{1 \over 4};{1 \over 4};{1 \over 4}} \right)\) ;
(C) G \(\left( {{2 \over 3};{2 \over 3};{2 \over 3}} \right)\) ; (D) G \(\left( {{1 \over 2};{1 \over 2};{1 \over 2}} \right)\).
Chọn (D) G \(\left( {{1 \over 2};{1 \over 2};{1 \over 2}} \right)\).
Bài 6: Trong không gian \(Oxyz\) cho bốn điểm \(A(1; 0; 0), B(0; 1; 0), C(0; 0; 1)\) và \(D(1; 1; 1)\)
Mặt cầu ngoại tiếp tứ diện \(ABCD\) có bán kính là:
Advertisements (Quảng cáo)
(A) \({{\sqrt 3 } \over 2}\) ; (B) \(\sqrt2\) ;
(C) \(\sqrt3\); (D) \({3 \over 4}\) .
Phương trình tổng quát của mặt cầu là:
\({x^2} + {y^2} + {z^2} – 2ax – 2by – 2cz + d = 0\)
Mặt cầu đi qua \(A,B,C,D\) nên ta có hệ:
\(\left\{ \matrix{
1 – 2a + d = 0(1) \hfill \cr
1 – 2b + d = 0(2) \hfill \cr
1 – 2c + d = 0(3) \hfill \cr
3 – 2a – 2b – 2c + d = 0(4) \hfill \cr} \right.\)
Lấy (1)+(2)+(3)-(4) ta được: \( \Rightarrow d = 0\)
Từ đây ta được: \(a = {1 \over 2},b = {1 \over 2},c = {1 \over 2}\)
\({R} = \sqrt {{a^2} + {b^2} + {c^2} – d} = {{\sqrt 3 } \over 2}\)
Chọn (A) \({{\sqrt 3 } \over 2}\).
Bài 7: Cho mặt phẳng \((α)\) đi qua điểm \(M(0 ; 0 ; -1)\) và song song với giá của hai vectơ \(\overrightarrow a = \left( {1; – 2;3} \right)\) và \(\overrightarrow b = (3 ; 0 ; 5)\).
Phương trình của mặt phẳng \((α)\) là:
(A) \(5x – 2y – 3z – 21 = 0\) ;
(B) \( – 5x + 2y + 3z + 3 = 0\) ;
(C) \(10x – 4y – 6z + 21 = 0\) ;
(D) \(5x – 2y – 3z + 21 = 0\) .
Gọi \(\vec n\) là véc tơ pháp tuyến của mặt phẳng \((\alpha)\) thì
\(\overrightarrow n = \left[ {\overrightarrow a ;\overrightarrow b } \right] = ( – 10;4;6)\).
Phương trình của mặt phẳng \((\alpha)\) là:
\(- 10(x – 0) + 4(y – 0) + 6(z + 1) = 0\)
\(\Leftrightarrow 10x + 4y + 6z + 6 = 0 \)
\(\Leftrightarrow – 5x + 2y + 3z + 3 = 0\)
Chọn (B) \( – 5x + 2y + 3z + 3 = 0\).
Bài 8: Cho ba điểm \(A (0 ; 2 ; 1), B(3; 0 ;1), C(1 ; 0 ; 0)\). Phương trình mặt phẳng \((ABC)\) là:
(A) \(2x – 3y – 4z +2 = 0\)
(B) \(2x + 3y – 4z – 2 = 0\)
(C) \(4x + 6y – 8z + 2 = 0\)
(D) \(2x – 3y – 4z + 1 = 0\).
Advertisements (Quảng cáo)
\(\overrightarrow {AB} = (3; – 2;0),\overrightarrow {AC} = (1; – 2; – 1)\)
Véc tơ pháp tuyến của mặt phẳng \((ABC)\) là:
\(\overrightarrow n = \left[ {\overrightarrow {AB} ;\overrightarrow {AC} } \right] = (2; – 3; – 4)\)
Phương trình mặt phẳng \((ABC)\) là:
\(2(x – 0) + 3(y – 2) – 4(z – 1) = 0 \)
\(\Leftrightarrow 2x + 3y – 4z – 2 = 0\)
Chọn (B) \(2x + 3y – 4z – 2 = 0\).
Bài 9: Gọi \((α)\) là mặt phẳng cắt ba trục toạ độ tại \(3\) điểm \(M(8 ; 0 ; 0), N(0 ; -2 ; 0), P(0 ; 0 ; 4)\). Phương trình của \((α)\) là:
(A) \({x \over 8} + {y \over { – 2}} + {z \over 4} = 0\);
(B) \({x \over 4} + {y \over { – 1}} + {z \over 2} = 1\);
(C) \(x – 4y + 2z = 0\);
(D) \(x – 4y + 2z – 8 = 0\).
Phương trình mặt phẳng \((\alpha)\) dưới dạng đoạn chắn là:
\({x \over 8} + {y \over { – 2}} + {z \over 4} = 1 \Leftrightarrow x – 4y + 2z – 8 = 0\)
Chọn (D) \(x – 4y + 2z – 8 = 0\).
Bài 10: Cho ba mặt phẳng \((α)\) \(x + y + 2z + 1 = 0\);
\((β)\) \(x + y – z + 2 = 0\);
\((γ)\) \(x – y + 5 = 0\).
Trong các mệnh đề sau, mệnh đề nào sai?
(A) \((α) ⊥ (β)\) ; (B) \((γ) ⊥ (β)\);
\((C) (α)// (γ)\) ; (D) \((α) ⊥ (γ)\).
Chọn (C) \((α) //(γ)\).
Bài 11: Cho đường thẳng \(△\) đi qua điểm \(M(2 ; 0 ; -1)\) và có vectơ chỉ phương \(\overrightarrow a = (4 ; -6 ; 2)\). Phương trình tham số của đường thẳng \(△\) là:
\((A)\left\{ \matrix{
x = – 2 + 4t \hfill \cr
y = – 6t \hfill \cr
z = 1 + 2t \hfill \cr} \right.\)
\((B)\left\{ \matrix{
x = – 2 + 2t \hfill \cr
y = – 3t \hfill \cr
z = 1 + t \hfill \cr} \right.\);
\((C)\left\{ \matrix{
x = 2 + 2t \hfill \cr
y = – 3t \hfill \cr
z = – 1 + t \hfill \cr} \right.\);
\((D)\left\{ \matrix{
x = 4 + 2t \hfill \cr
y = – 6 – 3t \hfill \cr
z = 2 + t \hfill \cr} \right.\).
Chọn (C) \(\left\{ \matrix{
x = 2 + 2t \hfill \cr
y = – 3t \hfill \cr
z = – 1 + t \hfill \cr} \right.\)
Bài 12: Cho \(d\) là đường thẳng đi qua điểm \(A(1 ; 2 ; 3)\) và vuông góc với mặt phẳng \((α): 4x + 3y – 7z + 1 = 0\).
Phương trình tham số của d là:
(A)\(\left\{ \matrix{
x = – 1 + 4t \hfill \cr
y = – 2 + 3t \hfill \cr
z = – 3 – 7t \hfill \cr} \right.\);
(B)\(\left\{ \matrix{
x = 1 + 4t \hfill \cr
y = 2 + 3t \hfill \cr
z = 3 – 7t \hfill \cr} \right.\);
(C)\(\left\{ \matrix{
x = 1 + 3t \hfill \cr
y = 2 – 4t \hfill \cr
z = 3 – 7t \hfill \cr} \right.\);
(D)\(\left\{ \matrix{
x = – 1 + 8t \hfill \cr
y = – 2 + 6t \hfill \cr
z = – 3 – 14t. \hfill \cr} \right.\)
Đường thẳng \(d\) vuông góc với mặt phẳng \(\alpha\) nên có véc tơ chỉ phương là:
\(\vec u=(4;3;-7)\)
Phương trình tham số của \(d\) là:
\(\left\{ \matrix{
x = 1 + 4t \hfill \cr
y = 2 + 3t \hfill \cr
z = 3 – 7t \hfill \cr} \right.\)
Chọn (B)
Bài 13: Cho hai đường thẳng
d1 :\(\left\{ \matrix{
x = 1 + 2t \hfill \cr
y = 2 + 3t \hfill \cr
z = 3 + 4t \hfill \cr} \right.\)
và
d2:\(\left\{ \matrix{
x = 3 + 4k \hfill \cr
y = 5 + 6k \hfill \cr
z = 7 + 8k. \hfill \cr} \right.\)
Trong các mệnh đề sau, mệnh đề nào đúng?
(A) d1⊥ d2 (B) d1 // d2
(C) d1 ≡ d2 (D) d1 và d2 chéo nhau.
Chọn (C) d1 ≡ d2
Bài 14: Cho mặt phẳng \((α) : 2x + y + 3z + 1= 0\) và đường thẳng \(d\) có phương trình tham số :
\(\left\{ \matrix{
x = – 3 + t \hfill \cr
y = 2 – 2t \hfill \cr
z = 1. \hfill \cr} \right.\)
Trong các mệnh đề sau, mệnh đề nào đúng?
(A) \(d ⊥ (α)\) ;
(B) \(d\) cắt \( (α)\) ;
(C) \(d // (α)\) ;
(D) \(d ⊂ (α)\).
Mặt phẳng \((\alpha)\) có véc tơ pháp tuyến \(\vec n=(2;1;3)\)
Đường thẳng \(d\) có véc tơ chỉ phương \(\vec u=(1;-2;0)\)
\(\vec n.\vec u=0\)
Chọn \(M(-3;2;1)\in d\) thay tọa độ của \(M\) vào phương trình mặt phẳng \((\alpha)\) ta được:ư
\(2.(-3)+2+3.1+1=0\) do đó \(M\in (\alpha)\)
Hay \(d ⊂ (α)\)
Chọn (D)
Bài 15: Cho \((S)\) là mặt cầu tâm \(I(2 ; 1 ; -1)\) và tiếp xúc với mặt phẳng \((α)\) có phương trình : \(2x – 2y – z + 3 = 0\).
Bán kính của \((S)\) là:
(A) \(2\) ; (B) \({2 \over 3}\); (C) \({4 \over 3}\); (D) \({2 \over 9}\) .
Bán kính của mặt cầu \((S)\) là:
\(r = d(I;(\alpha )) = {{\left| {2.2 – 2.1 – ( – 1) + 3} \right|} \over {\sqrt {{2^2} + {{( – 2)}^2} + {{( – 1)}^2}} }} = {6 \over 3} = 2\)
Chọn (A) 2.

