1. Khoanh vào chữ đặt trước câu trả lời đúng:
Các số: \(20 000; 14 075; 19 999; 30 009; 19 070\) được xếp theo thứ tự từ lớn đến bé là:
A) \(20 000; 30 009; 19 999; 19 070; 14 075\)
B) \(30 009; 20 000; 19 999; 19 070; 14 075\)
C) \(30 009; 19 999; 20 000; 19 070; 14 075\)
2. Khoanh vào chữ đặt trước câu trả lời đúng:
Các phân số \(\dfrac{3}{4};\dfrac{{100}}{{100}};\dfrac{{11}}{{12}};\dfrac{5}{3};\dfrac{7}{{15}}\) được xếp theo thứ tự từ lớn đến bé là:
A) \(\dfrac{5}{3};\dfrac{{100}}{{100}};\dfrac{{11}}{{12}};\dfrac{3}{4};\dfrac{7}{{15}}\)
B) \(\dfrac{5}{3};\dfrac{{11}}{{12}};\dfrac{{100}}{{100}};\dfrac{7}{{15}};\dfrac{3}{4}\)
C) \(\dfrac{{100}}{{100}};\dfrac{5}{3};\dfrac{{11}}{{12}};\dfrac{7}{{15}};\dfrac{3}{4}\)
3. Đúng ghi Đ, sai ghi S vào ô trống:
Trong các số \(4700; 61 059; 50 280; 6910\), số chia hết cho \(2\), cho \(3\) và cho \(5\) là:
|
\(4700\) |
|
|
\(50 280\) |
|
|
\(6910\) |
|
4. Đúng ghi Đ, sai ghi S vào ô trống:
Một trường học có \(945\) học sinh nữ và chiếm \(\dfrac{7}{{15}}\) tổng số học sinh toàn trường. Hỏi trường đó có bao nhiêu học sinh nam?
|
\(980\) |
|
|
\(1020\) |
|
|
\(1080\) |
|
|
\(2025\) |
|
5. Khoanh vào chữ đặt trước câu trả lời đúng:
Một hình vuông có cạnh \(1dm \;4cm\). Diện tích hình vuông đó là:
A) \(196cm^2\)
B) \(196dm^2\)
C) \(1dm^2 \;96cm^2\)
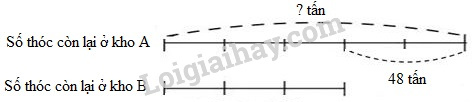
6. Kho A có số thóc nhiều hơn kho B là \(48\) tấn. Sau khi mỗi kho lấy ra \(24\) tấn thì số thóc còn lại ở kho A bằng \(\dfrac{5}{3}\) số thóc còn lại ở kho B. Tính số thóc lúc đầu ở mỗi kho.
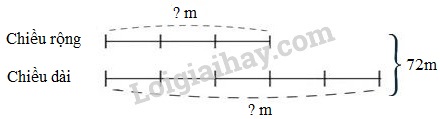
7. Một khu vườn hình chữ nhật có chu vi \(144m\), chiều rộng bằng \(\dfrac{3}{5}\) chiều dài. Tính diện tích khu vườn đó.

1.
Phương pháp:
So sánh các số đã cho rồi sắp xếp các số đó theo thứ tự từ lớn đến bé.
Cách giải:
Ta có: \(30 009 > 20 000 > 19 999 > 19 070 > 14 075\).
Vậy các số đã cho được sắp xếp theo thứ tự từ lớn đến bé là: \(30 009; 20 000; 19 999; 19 070; 14 075\).
Chọn B
2.
Phương pháp:
So sánh các phân số đã cho rồi sắp xếp các số đó theo thứ tự từ lớn đến bé.
Advertisements (Quảng cáo)
Cách giải:
Ta có: \(\dfrac{3}{4}<1\,;\;\;\dfrac{{100}}{{100}}=1\,;\;\;\dfrac{{11}}{{12}}<1;\) \(\dfrac{5}{3}>1\,;\;\;\dfrac{7}{{15}}<1\).
Ta sẽ so sánh các phân số \(\dfrac{3}{4};\;\dfrac{{11}}{{12}};\;\dfrac{7}{{15}}\).
Quy đồng mẫu số các phân số ta có:
\(\dfrac{3}{4}= \dfrac{3\times 15}{4 \times 15 }= \dfrac{45}{60};\) \(\dfrac{11}{12}= \dfrac{11\times5}{12 \times 5}= \dfrac{55}{60};\)
\(\dfrac{7}{15}= \dfrac{7\times 4}{15 \times 4}= \dfrac{28}{60};\)
Mà \(\dfrac{55}{60} > \dfrac{45}{60}>\dfrac{28}{60}\) , hay \(\dfrac{11}{12} > \dfrac{3}{4}>\dfrac{7}{15}\).
Vậy ta có: \(\dfrac{5}{3}>\dfrac{{100}}{{100}}>\dfrac{{11}}{{12}}>\dfrac{3}{4}>\dfrac{7}{{15}}\).
Các phân số đã cho được sắp xếp theo thứ tự từ lớn đến bé là: \(\dfrac{5}{3};\dfrac{{100}}{{100}};\dfrac{{11}}{{12}};\dfrac{3}{4};\dfrac{7}{{15}}\)
Chọn A
3.
Phương pháp:
– Các số có chữ số tận cùng là 0 thì chia hết cho cả \(2\) và \(5\).
– Các số có tổng các chữ số chia hết cho \(3\) thì chia hết cho \(3\).
Cách giải:
Trong các số 4700; 61 059; 50 280; 6910, số chia hết cho \(2\), cho \(3\) và cho \(5\) là:
|
\(4700\) |
S |
|
\(50 280\) |
Đ |
|
\(6910\) |
S |
4.
Phương pháp:
– Tìm số học sinh toàn trường ta lấy số học sinh nữ chia cho \(7\) rồi nhân với \(15\).
– Tìm số học sinh nam ta lấy số học sinh cả trường trừ đi số học sinh nữ.
Cách giải:
Advertisements (Quảng cáo)
Số học sinh cả trường là:
\(945:7 \times 15 = 2025\) (học sinh)
Số học sinh nam của trường đó là:
\(2025 – 945 = 1080\) (học sinh)
Ta có bảng sau
|
\(980 \) |
S |
|
\(1020\) |
S |
|
\(1080\) |
Đ |
|
\(2025\) |
S |
5.
Phương pháp:
Diện tích hình vuông = cạnh \(\times \) cạnh.
Cách giải:
Đổi: \(1dm\; 4cm = 14cm\)
Diện tích hình vuông là:
\(14 \times 14 = 196\; (cm^2)\)
Chọn A
6.
Phương pháp:
– Sau khi lấy mỗi kho ra \(24\) tấn thóc thì hiệu số thóc hai kho không đổi và bằng \(48\) tấn.
– Ta tìm số thóc còn lại của mỗi kho theo dạng toán tìm hai số khi biết hiệu và tỉ số của hai số đó.
– Tìm số thóc ban đầu ta lấy số thóc còn lại cộng với số thóc đã lấy ra.
Cách giải:
Sau khi lấy mỗi kho ra \(24\) tấn thóc thì hiệu số thóc hai kho không đổi và bằng \(48\) tấn.
Ta có sơ đồ:
Hiệu số phần bằng nhau là:
\(5 – 3 = 2\) (phần)
Kho A sau khi lấy đi 24 tấn còn số thóc là:
\(48:2 \times 5 = 120\) (tấn)
Kho A lúc đầu có số thóc là:
\(120 + 24 = 144\) (tấn)
Kho B lúc đầu có số thóc là:
\(144 – 48 = 96\) (tấn)
Đáp số: Kho A: \(144\) tấn;
Kho B: \(96\) tấn.
7.
Phương pháp:
– Tìm chiều dài, chiều rộng theo bài toán tìm hai số khi biết tổng và tỉ số của hai số đó.
– Diện tích = chiều dài \(\times \) chiều rộng.
Cách giải:
Nửa chu vi khu vườn hình chữ nhật là:
\(144:2 = 72\;(m)\)
Ta có sơ đồ:
Tổng số phần bằng nhau là:
\(5 + 3 = 8\) (phần)
Chiều rộng hình khu vườn hình chữ nhật là:
\(72:8 \times 3 = 27\;(m)\)
Chiều dài hình chữ nhật là:
\(72 – 27 = 45\;(m)\)
Diện tích khu vườn hình chữ nhật là:
\(45 \times 27 = 1215\;(m^2)\)
Đáp số: \(1215m^2\).