Cho tam giác ABC có ba góc nhọn (\(AB < AC\)), đường cao AD. So sánh \(\widehat {BA{\rm{D}}}\) và \(\widehat {DAC}\); so sánh DC và DB … trong Đề kiểm tra 15 phút Chương 3 Hình học 7. Xem Đề và đáp án đầy đủ phía dưới đây
Cho tam giác ABC có ba góc nhọn (\(AB < AC\)), đường cao AD.
a) So sánh \(\widehat {BA{\rm{D}}}\) và \(\widehat {DAC}\); so sánh DC và DB.
b) Lấy H thuộc đoạn thẳng DC, vẽ HK vuông góc với AC (K thuộc AC). Gọi E là giao điểm của AD và HK. Chứng minh \(AH \bot EC\).
Advertisements (Quảng cáo)
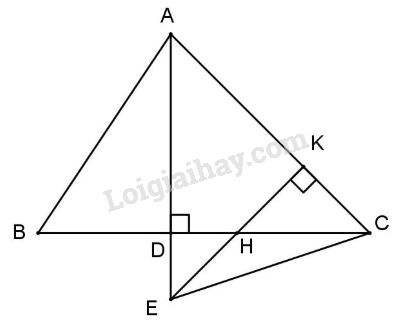
a) Ta có \(AB < AC\) (gt) \( \Rightarrow \widehat C < \widehat B\)
mà \(\widehat C + \widehat {DAC} = {90^0}\) và \(\widehat B + \widehat {BA{\rm{D}}} = {90^0}\)
\( \Rightarrow \widehat {DAC} > \widehat {BA{\rm{D}}}.\)
Vì \(AB < AC\) (gt) \( \Rightarrow DB < DC\) (quan hệ đường xiên hình chiếu).
b) Ta có EK và CD là hai đường cao của \(\Delta A{\rm{E}}C\) nên H là trực tâm \( \Rightarrow \) AH là đường cao thứ ba, hay \(AH \bot EC.\)
