
Cho tam giác ABC có ba góc nhọn, hai đường cao BH và CK. Trên tia đối của tia BH lấy D sao cho \(BD = AC\), trên tia đối của tia CK lấy điểm E sao cho \(CE = AB\). Chứng minh \(\Delta A{\rm{D}}E\) vuông cân.

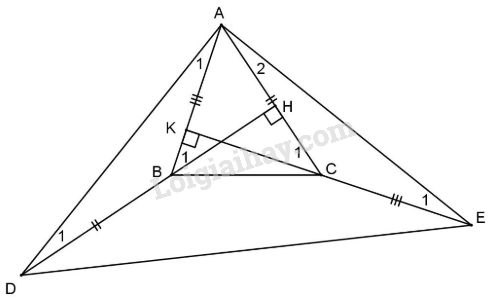
Ta có \({\widehat B_1} = {\widehat C_1}\) (cùng phụ với \(\widehat {BAC}\))
\( \Rightarrow \widehat {AB{\rm{D}}} = \widehat {AC{\rm{E}}}\) (kề bù với \({\widehat B_1} = {\widehat C_1}\))
Xét \(\Delta AB{\rm{D}}\) và \(\Delta EC{\rm{A}}\) có:
Advertisements (Quảng cáo)
+) \(AB = CE\) (gt);
+) \(\widehat {AB{\rm{D}}} = \widehat {AC{\rm{E}}}\) (cmt);
Advertisements (Quảng cáo)
+) \(BD = AC\) (gt);
Do đó \(\Delta AB{\rm{D}} = \Delta EC{\rm{A}}\) (c.g.c)
\( \Rightarrow {\widehat A_1} = {\widehat E_1}\) và \({\widehat A_3} = {\widehat D_1}\) (góc tương ứng).
\(\Delta ABH\) vuông tại H (gt)
\({\widehat B_1} + \widehat {BAC} = {90^0}\) mà \({\widehat B_1} = {\widehat A_1} + {\widehat D_1}\) (góc ngoài của \(\Delta AB{\rm{D}}\)) và \({\widehat D_1} = {\widehat A_2}\) (cmt).
Do đó \({\widehat A_1} + \widehat {BAC} + {\widehat A_2} = {90^0},\) lại có \(AD = AE\) (cmt).
Vậy \(\Delta A{\rm{D}}E\) vuông cân.

