
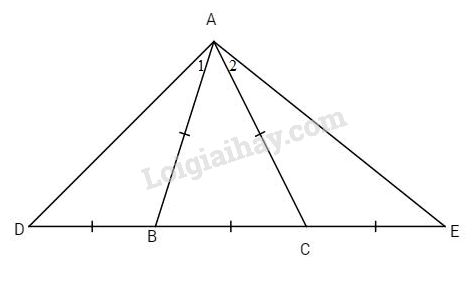
Cho tam giác ABC. Trên tia đối của tia BC lấy D, trên tia đối của tia CB lấy E sao cho \(\widehat {DAE} = \widehat {{A_1}} + \widehat {BAC} + \widehat {{A_2}} \)\(\,= {30^o} + {60^o} + {30^o} = {120^o}\) \(BD = CE = BC\) .
a) Chứng minh \(\Delta ADE\) cân.
b) Tính \(\widehat {DAE}\).

Advertisements (Quảng cáo)
a) \(\Delta ABC\) đều \( \Rightarrow AB = BC = AC\) và \(\widehat A = \widehat B = \widehat C = {60^o}\).
Mà \(BD = CE = BC\) (giả thiết) \( \Rightarrow AB = BD = BC = CE = AC\).
Advertisements (Quảng cáo)
Mặt khác \(\widehat {ABD} + \widehat {ABC} = {180^o}\) (kề bù)
Tương tự \(\widehat {ACE} + \widehat {ACB} = {180^o}\) mà \(\widehat {ABC} = \widehat {ACB} = {60^o}\)
\( \Rightarrow \widehat {ABD} = \widehat {ACE} = {120^o}\)
Do đó \(\Delta ABD = \Delta ACE\) (c.g.c) \( \Rightarrow AD = AE\) hay \(\Delta ADE\) cân tại A.
b) \(\Delta ABD\) cân có \(\widehat {ABD} = {120^o} \)\(\,\Rightarrow \widehat {{A_1}} = \widehat D =\dfrac {{{{180}^o} – {{120}^o}}}{2} = {30^o}\)
Tương tự ta có \(\widehat {{A_2}} = \widehat E = {30^o}\)
Vậy \(\widehat {DAE} = \widehat {{A_1}} + \widehat {BAC} + \widehat {{A_2}} \)\(\,= {30^o} + {60^o} + {30^o} = {120^o}\).

