
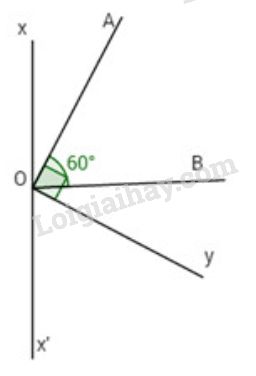
Cho góc \(\widehat {AOB} = {60^o}.\) Trên cùng nửa mặt phẳng bờ OB chứa OA, vẽ tia Ox vuông góc với tia OB. Trên nửa mặt phẳng kia, vẽ tia Oy vuông góc với OA.
a) Chứng minh \(\widehat {AOx} = \widehat {BOy}.\)
b) Vẽ Ox’ là tia đối của tia Ox. Hãy tính \(\widehat {x’Oy}.\)

Advertisements (Quảng cáo)
a) \(OB \bot O x\) nên \(\widehat {xOB} = {90^o}.\)
Vì OA, Ox cùng nằm trên nửa mặt phẳng bờ OB và \(\widehat {AOB} < \widehat {xOB}\left( {{{60}^o} < {{90}^o}} \right)\) nên tia OA nằm giữa hai tia Ox và OB. Ta có \(\widehat {AOx} + \widehat {AOB} = \widehat {xOB}\) hay \(\widehat {AOx} + {60^o} = {90^o}\)
Advertisements (Quảng cáo)
\( \Rightarrow \widehat {AOx} = {30^o}.\)
Ta có \(Oy \bot OA\) nên \(\widehat {AOy} = {90^o}.\) Vì OA và Oy nằm trên hai nửa mặt phẳng đối nhau có bờ là OB nên tia OB nằm giữa hai tia OA và Oy, ta có:
\(\widehat {AOB} + \widehat {BOy} = \widehat {AOy}\) hay \({60^o} + \widehat {BOy} = {90^o} \Rightarrow \widehat {BOy} = {30^o}.\)
Vậy \(\widehat {AOx} = \widehat {BOy} = {30^o}.\)
b) Vì Ox’ là tia đối của tia Ox nên \(\widehat {xOx’} = {180^o}.\) Ta có:
\(\widehat {xOA} + \widehat {AOB} + \widehat {BOy} + \widehat {yOx’} = {180^o}\)
\(\eqalign{ & {30^o} + {60^o} + {60^o} + \widehat {x’Oy} = {180^o} \cr & \Rightarrow \widehat {x’Oy} = {180^o} – {120^o} = {60^o}. \cr} \)

