Câu 1: Xem hình 1.a, b, c, d, e. Hỏi cặp góc nào đối đỉnh? Cặp góc nào không đối đỉnh? Vì sao?
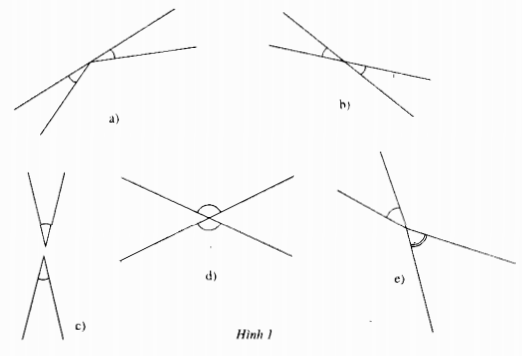
Hình a không phải là 2 góc đối đỉnh vì cạnh góc này không phải là tia đối cạnh góc kia.
Hình b là 2 góc đối đỉnh vì cạnh góc này là tia đối cạnh góc kia.
Hình c không phải là hai góc đối đỉnh vì chúng không chung đỉnh.
Hình d là hai góc đối đỉnh vì mỗi cạnh góc này là tia đối cạnh góc kia.
Hình e không phải là hai góc đối vì cạnh góc này không phải là tia đối cạnh góc kia.
Câu 2
a) Vẽ hai đường thẳng cắt nhau. Đặt tên cho các góc tạo thành.
b) Viết tên hai cặp góc đối đỉnh.
c) Viết tên các góc bằng nhau.
a) Hình vẽ:
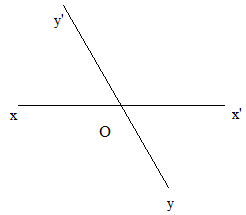
b) Góc xOy và x’Oy’ là cặp góc đối đỉnh.
Góc xOy’ và yOx’ là cặp góc đối đỉnh.
Advertisements (Quảng cáo)
c) \(\widehat {xOy} = \widehat {x’Oy’};\widehat {xOy’} = \widehat {{\rm{yOx’}}};\widehat {{\rm{xOx’}}} = \widehat {y{\rm{O}}y’} = 180^\circ \)
Câu 3
a) Vẽ góc xAy có số đo bằng \(50^\circ \).
b) Vẽ góc x’Ay’ đối đỉnh với góc xAy.
c) Vẽ tia phân giác At của góc xAy.
d) Vẽ tia đối At’ của tia At. Vì sao tia At’ là tia phân giác của góc x’Ay’?
e) Viết tên năm cặp góc đối đỉnh.
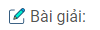
a) Vẽ \(\widehat {xAy} = 50^\circ \)
Advertisements (Quảng cáo)
b) Vẽ tia Ax’ là tia đối của tia Ax. Tia Ay’ là tia đối của tia Ay.
Góc x’Ay’ đối đỉnh với góc xAy
c) Hình vẽ trên.
d) Vì \(\widehat {xAt}\) và \(\widehat {x’At’}\) là cặp góc đối đỉnh nên \(\widehat {xAt} = \widehat {x’At’}\)
\(\widehat {tAy} = \widehat {t’Ay’}\) suy ra \(\widehat {x’At’} = \widehat {t’Ay’}\)
Vậy At’ là tia phân giác của góc \(\widehat {x’Ay’}\)
e) Tên 5 cặp góc đối đỉnh là: \(\widehat {xAy}\) và \(\widehat {x’Ay’}\); \(\widehat {xAy’}\) và \(\widehat {yAx’}\); \(\widehat {xAt}\) và \(\widehat {x’At’}\); \(\widehat {tAy}\) và \(\widehat {t’Ay’}\); \(\widehat {tAy’}\) và \(\widehat {yAt’}\).
Câu 4
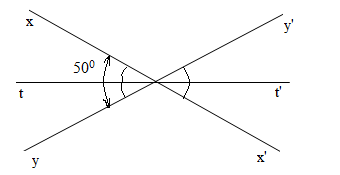
a) Vẽ đường tròn tâm O bán kính 2cm.
b) Vẽ góc AOB có số đo bằng \(60^\circ \). Hai điểm A, B nằm trên đường tròn (O; 2cm).
c) Vẽ góc BOC có số đo bằng \(60^\circ \). Điểm C thuộc đường tròn (O; 2cm).
d) Vẽ các tía OA’, OB’, OC’ lần lượt là tia đối của các tia OA, OB, OC. Các điểm A’; B’; C’ thuộc đường tròn (O; 2cm).
e) Viết tên năm cặp góc đối đỉnh.
g) Viết tên năm cặp góc bằng nhau mà không đối đỉnh.
a, b, c, d. Hình vẽ:
e) Tên 5 cặp góc đối đỉnh:
\(\widehat {AOB}\) và \(\widehat {A’OB’}\); \(\widehat {BOC}\) và \(\widehat {B’OC’}\);
\(\widehat {AOC}\) và \(\widehat {A’OC’}\); \(\widehat {AOB’}\) và \(\widehat {BOA’}\);
\(\widehat {AOC’}\) và \(\widehat {A’OC}\)
g) Vì \(\widehat {AOB} + \widehat {BOC} + \widehat {COA} = 180^\circ \) (Kề bù)
\( \Rightarrow \widehat {COA’} = 180^\circ – 60^\circ – 60^\circ = 60^\circ \)
Tên 5 cặp góc bằng nhau không đối đỉnh:
\(\eqalign{
& \widehat {AOB} = \widehat {BOC} = 60^\circ ;\widehat {BOC} + \widehat {COA’} = 60^\circ \cr
& \widehat {AOB} = \widehat {COA’} = 60^\circ ;\widehat {A’OB’} = \widehat {B’OC’} = 60^\circ \cr
& \widehat {AO{\rm{A}}’} = \widehat {BOB’} = 180^\circ \cr} \)

