Bài 5.1: a) Xác định a, b, c, d để đồ thị của các hàm số:
y = x2 + ax + b và y = cx + d
cùng đi qua hai điểm M(1; 1) và B(3; 3).
b) Vẽ đồ thị của các hàm số ứng với các giá trị a, b, c và d tìm được trên cùng một mặt phẳng tọa độ. Tính diện tích của hình phẳng giới hạn bởi hai đường cong trên.
c) Tính thể tích của vật thể tròn xoay sinh bởi hình phẳng trên quay quanh trục hoành.

a) a và b thỏa mãn hệ phương trình :
\(\left\{ {\matrix{{1 + a + b = 1} \cr {9 + 3a + b = 3} \cr} } \right. \Leftrightarrow \left\{ {\matrix{{a + b = 0} \cr {3a + b = – 6} \cr} } \right. \Leftrightarrow\left\{ {\matrix{{a = – 3} \cr {b = 3} \cr} } \right.\)
c và d thỏa mãn hệ phương trình:
\(\left\{ {\matrix{{c + d = 1} \cr {3c + d = 3} \cr} \Leftrightarrow \left\{ {\matrix{{c = 1} \cr {d = 0} \cr} } \right.} \right.\)
b) (H.90) Ta có hai hàm số tương ứng là: y = x2 – 3x + 3 và y = x
Vậy \(S = \int\limits_1^3 {( – {x^2} + 4x – 3)dx} = {4 \over 3}\) (đơn vị diện tích)
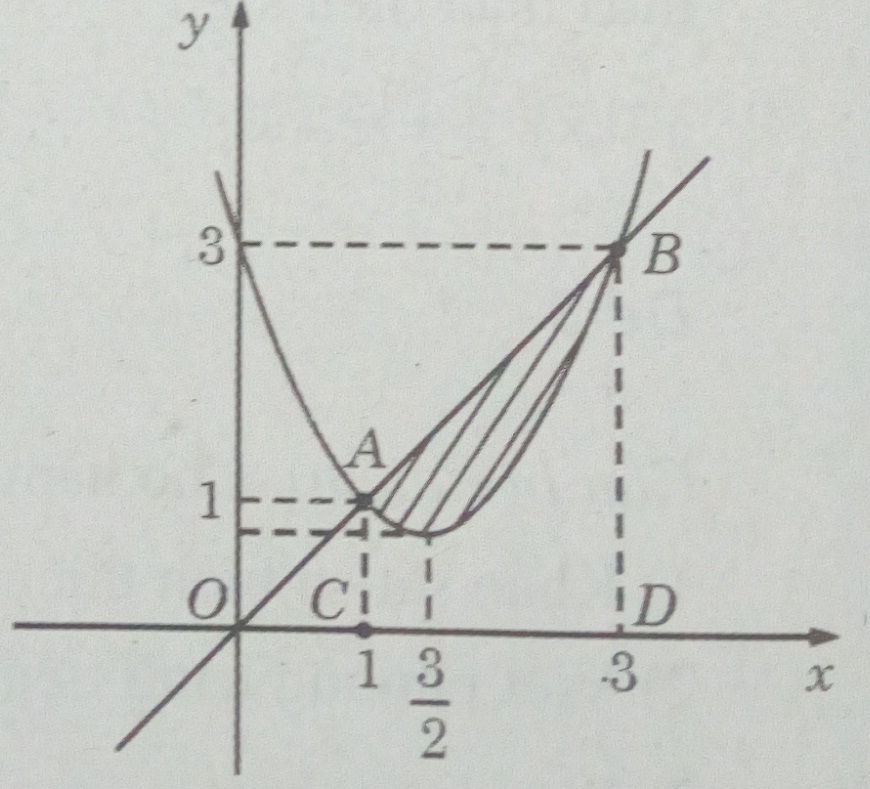
c) V = V1 – V2 , trong đó V1 là thể tích vật thể tròn xoay sinh ra do quay hình thang ACDB quanh trục Ox , V2 là thể tích vật thể tròn xoay sinh ra do quay hình thang cong ACDB quanh trục Ox.
Ta có \({V_1} = \pi \int\limits_1^3 {{x^2}dx = {{26} \over 3}\pi } \)
\({V_2} = \pi \int\limits_1^3 {{{({x^2} – 3x + 3)}^2}dx = {{22} \over 5}\pi } \)
Vậy \(V = {{26} \over 3}\pi – {{22} \over 5}\pi = {{64} \over {15}}\pi \) (đơn vị thể tích)
Bài 5.2: a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số: \(y = {{ – x + 2} \over {x + 2}}\)
b) Viết phương trình tiếp tuyến của (C) , biết nó vuông góc với đường thẳng \(y = {1 \over 4}x – 42\)

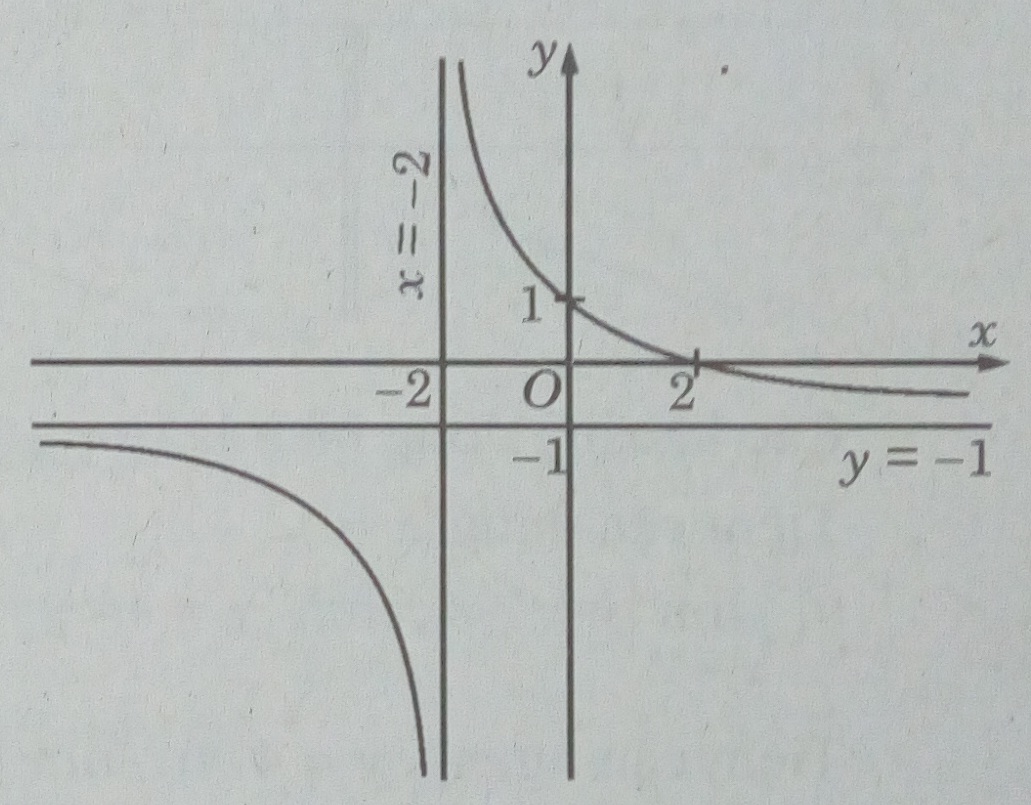
a) \(y = {{ – x + 2} \over {x + 2}}\)
Advertisements (Quảng cáo)
+) Tập xác định: D = R\{-2}
+) Ta có: \(y’ = – {4 \over {{{(x + 2)}^2}}}\)
Bảng biến thiên:
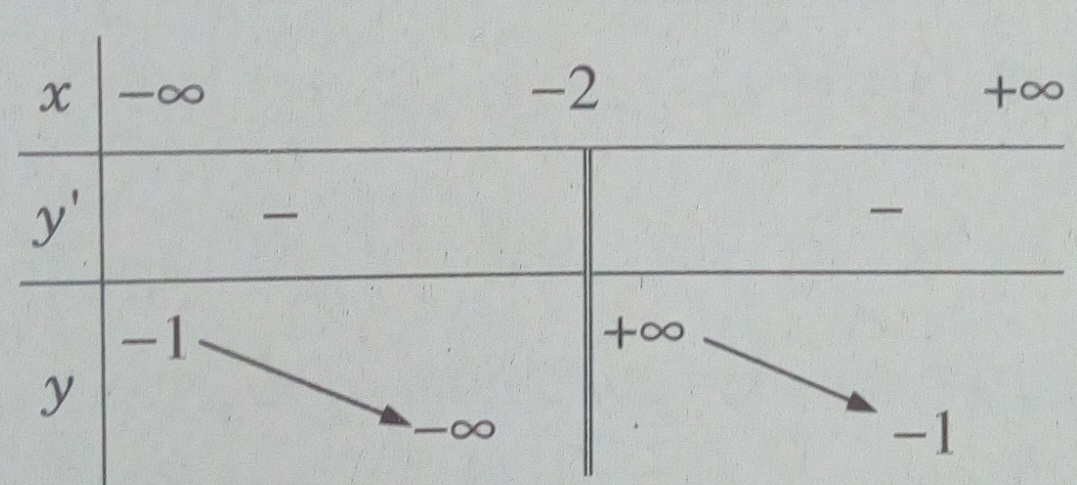
Hàm số nghịch biến trên các khoảng \(( – \infty ; – 2),( – 2; + \infty )\)
+) Tiệm cận đứng x = -2 vì \(\mathop {\lim }\limits_{x \to – {2^ + }} y = + \infty ,\mathop {\lim }\limits_{x \to – {2^ – }} y = – \infty \)
Tiệm cận ngang y = -1 vì \(\mathop {\lim }\limits_{x \to \pm \infty } y = – 1\)
Giao với các trục tọa độ: (0; 1); (2; 0)
Đồ thị
b) Tiếp tuyến của đồ thị có hệ số góc k = -4 (vì vuông góc với đường thẳng \(y = {1 \over 4}x – 42\) )
Hoành độ tiếp điểm thỏa mãn phương trình:
Advertisements (Quảng cáo)
\({{ – 4} \over {{{(x + 2)}^2}}} = – 4 = > \left[ {\matrix{{{x_1} = – 3} \cr {{x_2} = – 1} \cr} } \right.\)
Ứng với \({x_1} = – 3\) ,ta có tiếp tuyến y = – 4x – 17
Ứng với \({x_2} = – 1\), ta có tiếp tuyến y = – 4x – 1.
Bài 5.3: a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số : \(y = {{4x – 5} \over {x – 1}}\)
b) Tính diện tích hình phẳng giới hạn bởi (C), tiếp tuyến của (C) tại A(2; 3) và đường thẳng x = 4.

a) Tập xác định: D = R\{1}
Đạo hàm: \(y’ = {1 \over {{{(x – 1)}^2}}}\)
Bảng biến thiên:
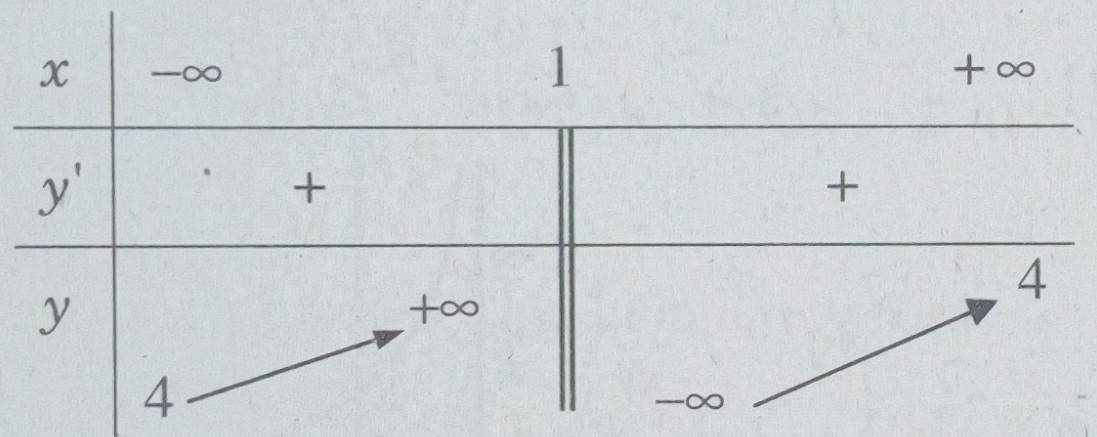
Các khoảng đồng biến là \(( – \infty ;1)\) và \((1; + \infty )\) :
Tiệm cận đứng x = 1 vì \(\mathop {\lim }\limits_{x \to {1^ + }} y = – \infty ;\mathop {\lim }\limits_{x \to {1^ – }} y = + \infty \)
Tiệm cận ngang y = 4 vì \(\mathop {\lim }\limits_{x \to \pm \infty } y = 4\)
Giao với các trục tọa độ: (0; 5) và \(({5 \over 4};0)\)
Đồ thị
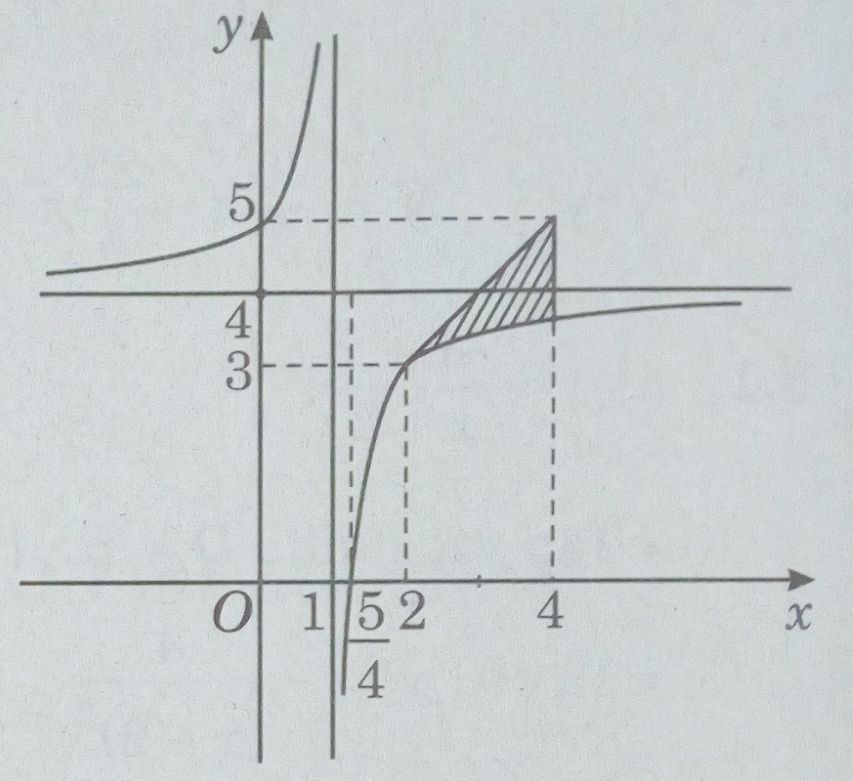
b) Ta có: y’(2) = 1. Phương trình tiếp tuyến là y = x + 1
Diện tích của miền cần tìm là:
\(S = \int\limits_2^4 {(x + 1 – 4 + {1 \over {x – 1}})dx} = \int\limits_2^4 {(x – 3 + {1 \over {x – 1}})dx} = \ln 3\).
Bài 5.4: Tìm các đường tiệm cận của đồ thị các hàm số sau:
a) \(y = {{5x + 3} \over { – x + 2}}\)
b) \(y = {{ – 6x + 2} \over {x – 1}}\)
c) \(y = {{2{x^2} + 8x – 9} \over {3{x^2} + x – 4}}\)
d) \(y = {{x + 2} \over { – 2x + 5}}\)

a) Tiệm cận đứng: x = 2; Tiệm cận ngang: y = -5
b) Tiệm cận đứng: x = 1 ; Tiệm cận ngang: y = -6
c) Ta có: \(\mathop {\lim }\limits_{x \to \pm \infty } {{2{x^2} + 8x – 9} \over {3{x^2} + x – 4}} = \mathop {\lim }\limits_{x \to \pm \infty } {{{x^2}(2 + {8 \over x} – {9 \over {{x^2}}})} \over {{x^2}(3 + {1 \over x} – {4 \over {{x^2}}})}} = {2 \over 3}\)
Vậy đồ thị có đường tiệm cận ngang \(y = {2 \over 3}\)
Ta có \(y = {{2{x^2} + 8x + 9} \over {(x – 1)(3x + 4)}}\)
Từ đó đồ thị có hai tiệm cận đứng là x = 1 và \(x = – {4 \over 3}\)
d) Tiệm cận đứng: \(x = {5 \over 2}\) . Tiệm cận ngang: \(y = – {1 \over 2}\)

