Bài 5.21: Tính diện tích của hình phẳng giới hạn bởi các đường sau:
a) y = |x2 – 1| và y = 5 + |x|
b) 2y = x2 + x – 6 và 2y = -x2 + 3x + 6
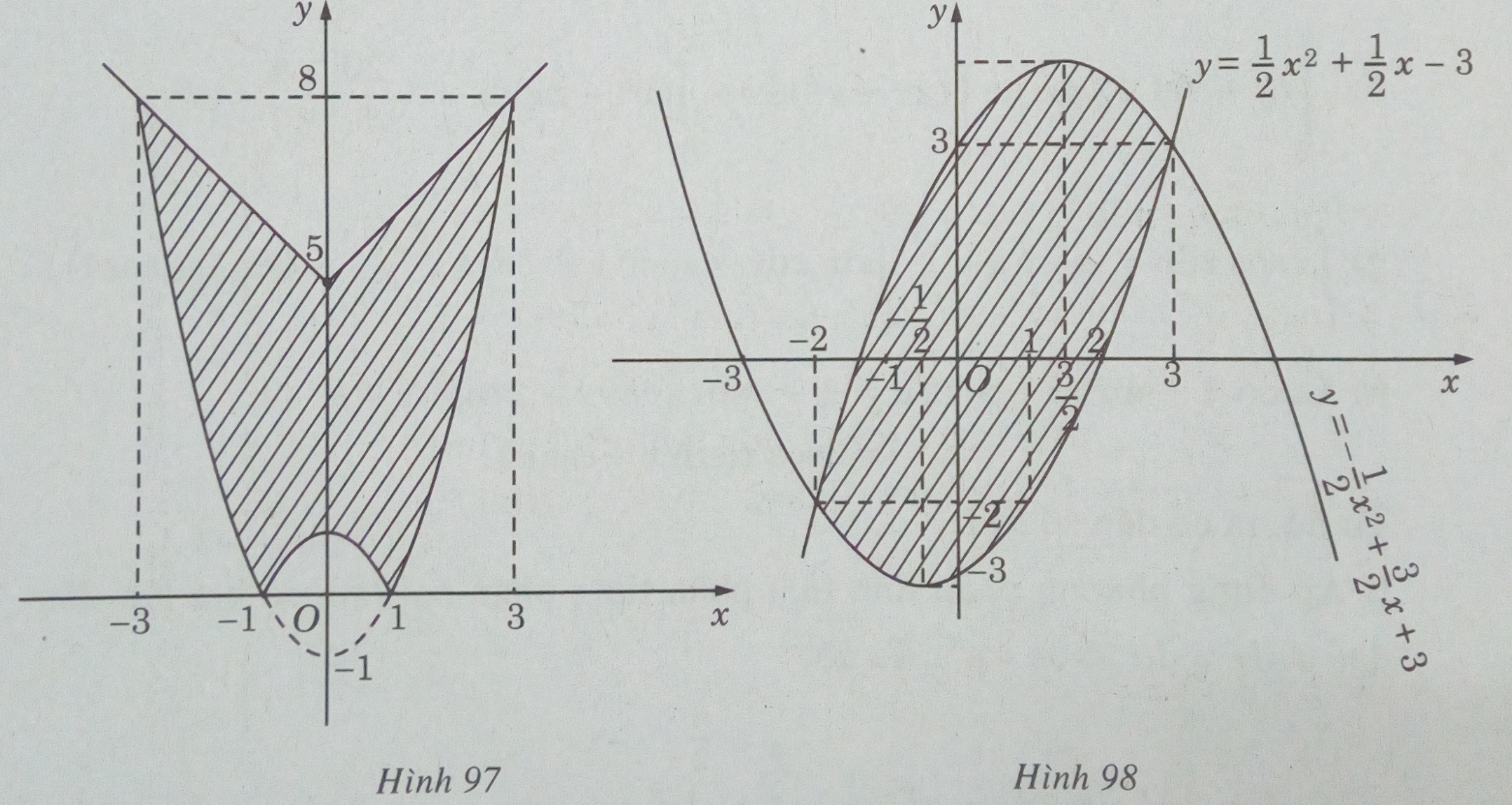
c) \(y = {1 \over x} + 1,x = 1\) và tiếp tuyến với đường \(y = {1 \over x} + 1\) tại điểm \((2;{3 \over 2})\)
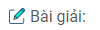
a) Hai hàm số y = |x2 – 1| và y = 5 + |x| đều là hàm số chẵn. Miền cần tính diện tích được thể hiện ở hình 97. Do tính đối xứng qua trục tung, ta có:
\(S = 2\int\limits_0^3 {(5 + |x| – |{x^2} – 1|)dx}\)
\( = 2\left[ {\int\limits_0^1 {(5 + x – 1 + {x^2})dx + \int\limits_1^3 {(5 + x – {x^2} + 1)dx} } } \right]\)
\( = 2\left[ {({1 \over 3}{x^3} + {1 \over 2}{x^2} + 4x)\left| {\matrix{1 \cr 0 \cr} + ( – {1 \over 3}{x^3} + {1 \over 2}{x^2} + 6x)\left| {\matrix{3 \cr 1 \cr} } \right.} \right.} \right]\)
\(= 24{1 \over 3}\) (đơn vị diện tích)
b) Miền cần tính diện tích được thể hiện bởi Hình 98 (học sinh tự làm)
Như vậy, với mọi \(x \in ( – 2;3)\) đồ thị của hàm số \(y = – {1 \over 2}{x^2} + {3 \over 2}x + 3\) nằm phía trên đồ thị của hàm số \(y = {1 \over 2}{x^2} + {1 \over 2}x – 3\).
Vậy ta có:
\(S = \int\limits_{ – 2}^3 {\left[ {( – {1 \over 2}{x^2} + {3 \over 2}x + 3) – ({1 \over 2}{x^2} + {1 \over 2}x – 3)} \right]} dx\)
\(= \int\limits_{ – 2}^3 {( – {x^2} + x + 6)} dx = 20{5 \over 6}\) (đơn vị diện tích)
c) Miền cần tính diện tích được thể hiện trên hình:
\(S = \int\limits_1^2 {\left[ {{1 \over x} + 1 – ( – {1 \over 4}x + 2)} \right]} dx\)
\(= \int\limits_1^2 {({1 \over x} + {1 \over 4}x – 1)dx = \ln 2 – {5 \over 8}} \)(đơn vị diện tích)
(vì tiếp tuyến với đồ thị của \(y = {1 \over x} + 1\) tại điểm \((2;{3 \over 2})\) có phương trình là \(y = f'(2)(x – 2) + {3 \over 2} = – {1 \over 4}x + 2\))
Bài 5.22: Tính thể tích của vật thể tròn xoay khi quay các hình phẳng giới hạn bởi các đường sau quanh trục Ox:
a) y = x3 ; y = 1 và x = 3
Advertisements (Quảng cáo)
b) \(y = {2 \over \pi }x;y = \sin x;x \in {\rm{[}}0;{\pi \over 2}{\rm{]}}\)
c) \(y = {x^\alpha },\alpha \in {N^*};y = 0;x = 0\) và x = 1

a)
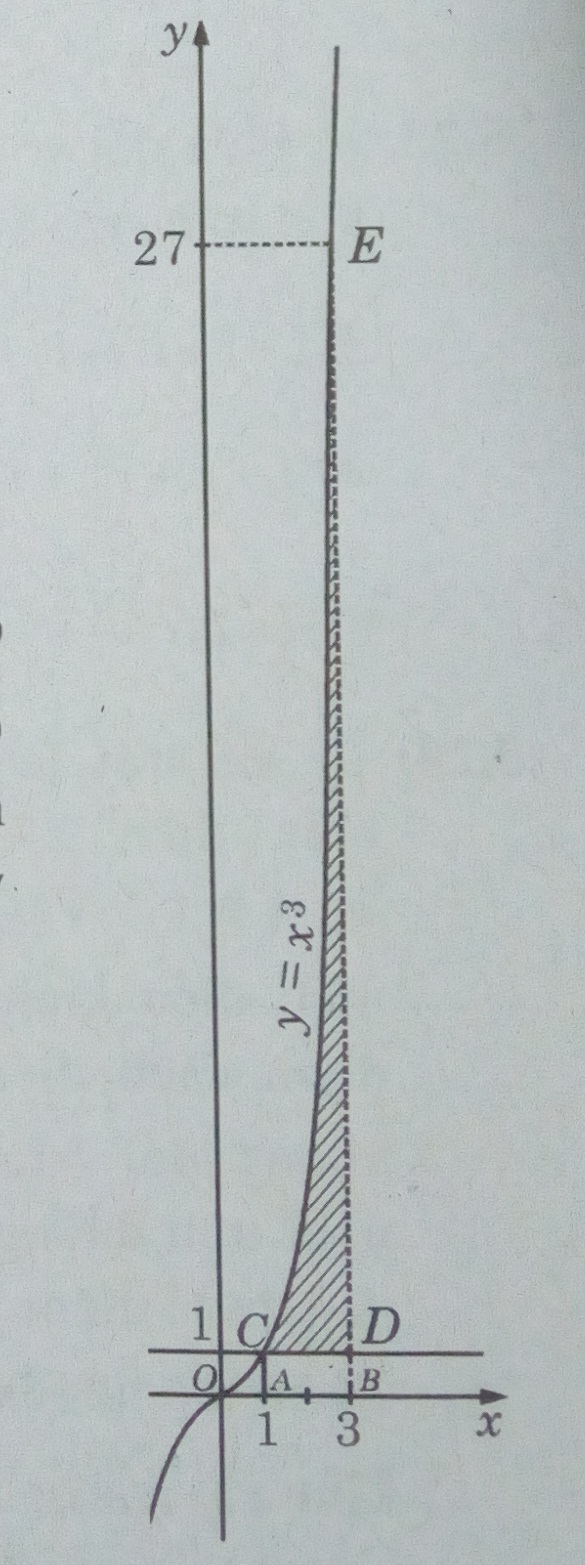
Thể tích vật thể tròn xoay sinh ra bởi miền CED quay quanh trục Ox là hiệu của hai thể tích (V1 và V2) của hai vật thể tròn xoay tương ứng sinh ra khi miền ACEB và miền ACDB quay quanh trục Ox. Như vậy V = V1 – V2 , trong đó :
\({V_1} = \pi \int\limits_1^3 {{x^6}} dx = {1 \over 7}\pi {x^7}\left| {\matrix{3 \cr 1 \cr} } \right. = {\pi \over 7}({3^7} – 1)\)
\({V_2} = \pi \int\limits_1^3 {dx = 2\pi }\)
\(\Rightarrow V = {V_1} – {V_2} = {\pi \over 7}({3^7} – 15) = 310{2 \over 7}\pi \) (đơn vị thể tích)
b)

Ta có V = V1 – V2 trong đó
\({V_1} = \pi \int\limits_0^{{\pi \over 2}} {{{\sin }^2}xdx} = {{{\pi ^2}} \over 4}\)
\({V_2} = \pi \int\limits_0^{{\pi \over 2}} {{{({2 \over \pi }x)}^2}dx = {{{\pi ^2}} \over 6}} \)
Advertisements (Quảng cáo)
\(V = {V_1} – {V_2} = {{{\pi ^2}} \over {12}}\) (đơn vị thể tích)
c) Hình vẽ
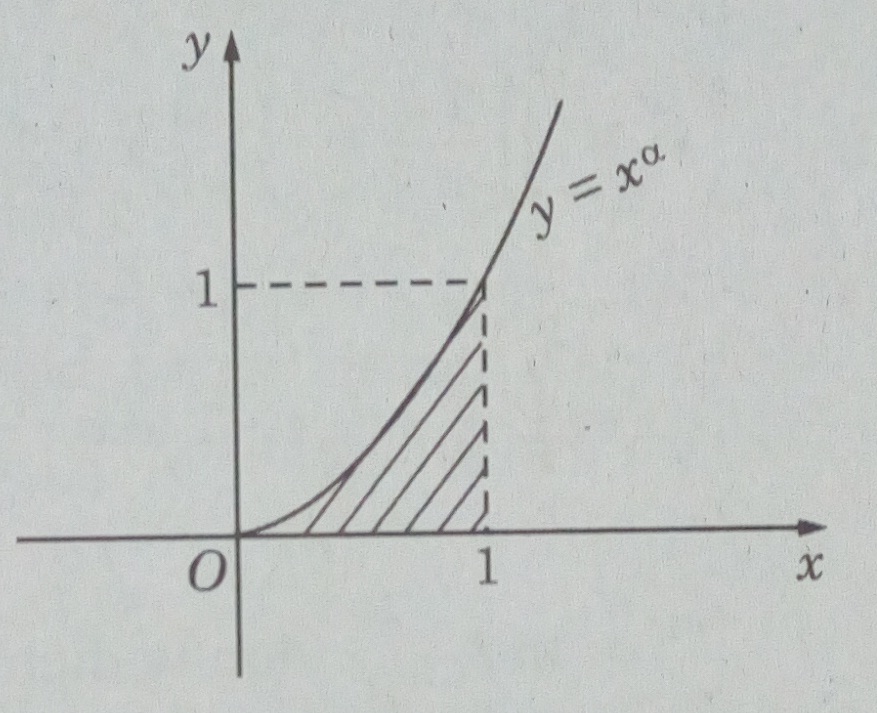
\(V = \pi \int\limits_0^1 {{x^{2\alpha }}dx} = {\pi \over {2\alpha + 1}}\)
Bài 5.23: Chứng minh rằng:
a) \(i + {i^2} + {i^3} + … + {i^{99}} + {i^{100}} = 0\)
b) \({{(\sqrt 2 + i)(1 – i)(1 + i)} \over i} = 2 – 2\sqrt 2 i\)

a) Biến đổi vế trái bằng cách nhóm từng bốn số hạng và đặt thừa số chung, ta được
\(i(1 + i + {i^2} + {i^3}) + … + {i^{97}}(1 + i + {i^2} + {i^3})\)
\(= (1 + i + {i^2} + {i^3})(i + … + {i^{97}}) = 0\),
Vì \(1 + i + {i^2} + {i^3} = 1 + i – 1 – i = 0\)
b) Ta có
\({{(\sqrt 2 + i)(1 – i)(1 + i)} \over i} \)
\(= {{2(\sqrt 2 + i)i} \over { – 1}}\)
\(= – (2\sqrt 2 i + 2{i^2}) = 2 – 2\sqrt 2 i\)
Bài 5.24: Tìm tập hợp các điểm biểu diễn số phức z trên mặt phẳng tọa độ thỏa mãn các điều kiện:
a) |z – i| = 1
b) |2 + z| < |2 – z|
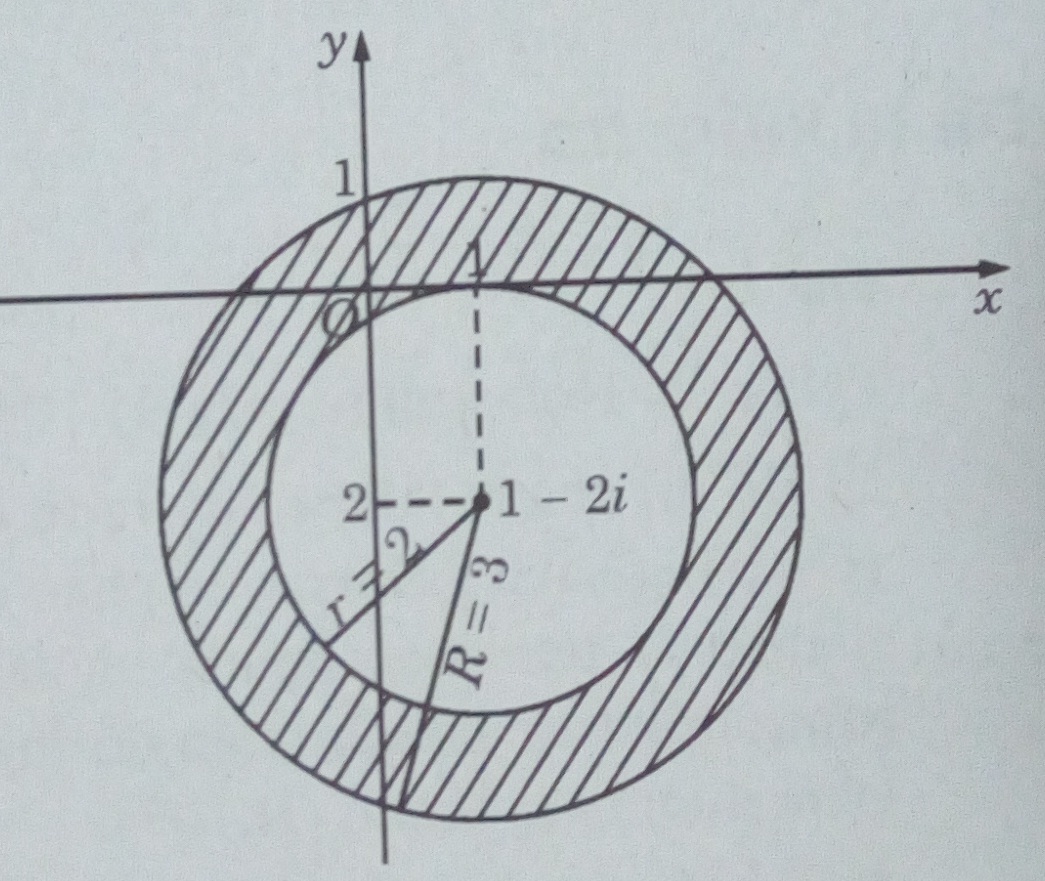
c) \(2 \le |z – 1 + 2i| < 3\)
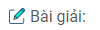
a) Vế trái là khoảng cách từ điểm biểu diễn z dến điểm biểu diễn z0 = 0 + i . Vậy tập hợp các điểm thỏa mãn điều kiện đã cho là tất cả các điểm cách điểm (0; 1) một khoảng không đổi bằng 1. Đó là các điểm nằm trên đường tròn bán kính bằng 1 và tâm là điểm (0; 1)
Ta có thể tiến hành như sau:
Cho \(z = x + iy\) , ta có \(|z – i{|^2} = |x + (y – 1)i{|^2} = {x^2} + {(y – 1)^2}\) và như vậy ta có: \({x^2} + {(y – 1)^2} = 1\)
Đây là phương trình đường tròn bán kính bằng 1 và tâm là (0; 1)
b)

Ta có: \(|2 + z{|^2} < |2 – z{|^2}\)
\(\Leftrightarrow |(2 + x) + iy{|^2} < |(2 – x) – iy{|^2}\)
\(\Leftrightarrow {(2 + x)^2} + {y^2} < {(2 – x)^2} + {( – y)^2}\)
\(\Leftrightarrow x < 0\)
Đó là tập hợp các số phức có phần thực nhỏ hơn 0, tức là nửa trái của mặt phẳng tọa độ không kể trục Oy.
c) Đó là những điểm nằm phía trong hình tròn bán kính bằng 3 và phía ngoài (kể cả biên) hình tròn bán kính bằng 2 có cùng tâm là điểm biểu diễn số phức z0 = 1 – 2i , tức là những điểm nằm trong hình vành khăn kể cả biên trong. Đó là những điểm (x; y) trên mặt phẳng tọa độ thỏa mãn điều kiện: \(4 \le {(x – 1)^2} + {(y + 2)^2} < 9\)