Bài 2.30: Cho đường tròn tâm O bán kính r’. Xét hình chóp S.ABCD có SA vuông góc với mặt phẳng đáy, S và A cố định, SA = h cho trước và có đáy ABCD là một tứ giác tùy ý nội tiếp đường tròn đã cho, trong đó các đường chéo AC và BD vuông góc với nhau.
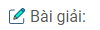
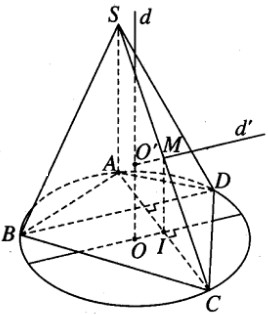
a) Trong mặt phẳng chứa đường tròn tâm O ngoại tiếp tứ giác ABCD ta kẻ đường kính qua O vuông góc với dây cung AC tại I. Ta có IA = IC và OI // BD. Gọi O’ là tâm mặt cầu đi qua 5 đỉnh của hình chóp. Khi đó điểm O’ phải nằm trên trục d của đường tròn ngoại tiếp tứ giác ABCD. Ta có \(d \bot (ABCD)\) tại O. Gọi M là trung điểm của cạnh SC. Ta có MI // SA nên \(MI \bot (ABCD)\) tại I. Từ M kẻ đường thẳng d’//OI cắt d tại O’. Vì \(d’ \bot (SAC)\) tại M nên ta có O’C = O’S và O’C là bán kính r của mặt cầu ngoại tiếp hình chóp S.ABCD
Ta có \(r = O’C = \sqrt {OO{‘^2} + O{C^2}} = \sqrt {M{I^2} + r{‘^2}}\)
\( = \sqrt {{{({h \over 2})}^2} + r{‘^2}} = {{\sqrt {{h^2} + 4r{‘^2}} } \over 2}\)
Vì SA không đổi nên ta có VSABCD lớn nhất khi và chỉ khi SABCD lớn nhất. Ta có \({S_{ABCD}} = {1 \over 2}AC.BD\) trong đó AC và BD là hai dây cung vuông góc với nhau. Vậy AC.BD lớn nhất khi và chỉ khi AC = BD = 2r’ , nghĩa là tứ giác ABCD là một hình vuông.
Bài 2.31: Cho hình lập phương ABCD.A’B’C’D’ cạnh a.
a) Tính diện tích xung quanh của hình trụ có đường tròn hai đáy ngoại tiếp các hình vuông ABC.D và A’B’C’D’.
b) Tính diện tích mặt cầu đi qua tất cả các đỉnh của hình lập phương.
Advertisements (Quảng cáo)
c) Tính diện tích xung quanh của hình nón tròn xoay nhận đường thẳng AC’ làm trục và sinh ra bởi cạnh AB.
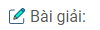
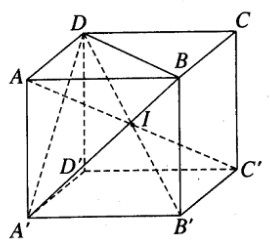
a) Hình trụ có chiều cao h = a và bán kính đáy \(r = {{a\sqrt 2 } \over 2}\)
Do đó ta có: \({S_{xq}} = 2\pi rh = \pi {a^2}\sqrt 2 \)
Advertisements (Quảng cáo)
b) Gọi I là tâm của hình lập phương. Tất cả các đỉnh của hình lập phương đều có khoảng cách đến I bằng \({{a\sqrt 3 } \over 2}\) nên chúng nằm trên mặt cầu tâm I bán kính \(r = {{a\sqrt 3 } \over 2}\)
Ta có diện tích mặt cầu đó là \(S = 4\pi {r^2} = 3\pi {a^2}\)
c) Đường tròn đáy của hình nón tròn xoay đỉnh A tạo nên bởi cạnh AB là đường tròn ngoại tiếp tam giác đều A’BD, tam giác này có cạnh bằng \(a\sqrt 2 \) và có đường cao bằng \({{a\sqrt 6 } \over 2}\)
Do đó đường tròn đáy hình nón có bán kính \(r’ = {{a\sqrt 6 } \over 3}\) . Vậy hình nón tròn xoay này có đường sinh l = a và có diện tích xung quanh là \({S_{xq}} = \pi r’l = \pi .{{a\sqrt 6 } \over 3}.a = {{\pi {a^2}\sqrt 6 } \over 3}\).
Bài 2.32: Hình trụ tròn xoay có bán kính đáy bằng r, có chiều cao bằng 2r và có trục là OO’.
a) Chứng minh rằng mặt cầu đường kính OO’ tiếp xúc với hai mặt đáy của hình trụ và tiếp xúc với tất cả các đường sinh của mặt trụ.
b) Cắt hình trụ bởi một mặt phẳng song song với trục OO’ và cách trục một khoảng bằng \({r \over 2}\) . Tính diện tích thiết diện thu được.
c) Thiết diện nói trên cắt mặt cầu đường kính OO’ theo thiết diện là một đường tròn. Tính bán kính của đường tròn đó.

a) Vì các mặt đáy của hình trụ vuông góc với trục OO’ tại O và O’ nên chúng tiếp xúc với mặt cầu đường kính OO’.
Gọi I là trung điểm của đoạn OO’. Ta có I là tâm của mặt cầu. Kẻ IM vuông góc với một đường sinh nào đó (M nằm trên đường sinh) ta đều có IM = r là bán kính của mặt trụ đồng thời điểm M cũng thuộc mặt cầu. Vậy mặt cầu tiếp xúc với tất cả các đường sinh của mặt trụ.
b) Trên mặt đáy tâm O ta gọi H là trung điểm của bán kính OP. Qua H kẻ dây cung \(AB \bot OP\) và nằm trong đáy (O; r). Các đường sinh AD và BC cùng với các dây cung AB và DC (thuộc đáy (O’, r)) xác định cho ta thiết diện cần tìm là một hình chữ nhật. Gọi S là diện tích hình chữ nhật này, ta có: SABCD = AB.AD trong đó AD = 2r còn AB = 2AH. Vì H là trung điểm của OP nên ta tính được \(AB = r\sqrt 3 \) . Vậy \({S_{ABCD}} = 2{r^2}\sqrt 3 \).
c) Đường tròn giao tuyến của mặt cầu đường kính OO’ và mặt phẳng (ABCD) có bán kính bằng \({{AB} \over 2} = {{r\sqrt 3 } \over 2}\) . Đường tròn này có tâm là tâm của hình chữ nhật ABCD và tiếp xúc với hai cạnh AD, BC của hình chữ nhật đó.

