Bài 1.32: Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD, các mặt (SAB) và (SAD) vuông góc với đáy. Góc giữa mặt (SAC) và đáy bằng 600, AB = 2a , BC = a. Tính thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng AB và SC theo a.
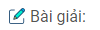
Vì các mặt (SAB) và (SAD) vuông góc với đáy nên \(SA \bot (ABCD)\) . Ta có:
\(\left\{ {\matrix{{BC \bot AB} \cr {BC \bot SA} \cr} } \right. \Rightarrow BC \bot (SAB)\)
⟹ góc\(((SBC),(ABCD)) = \widehat {SBA} = {60^0}\)
Do đó: \(SA = 2a\tan {60^0} = 2a\sqrt 3 \)
\({V_{S.ABCD}} = {1 \over 3}2a\sqrt 3 .2a.a = {{4\sqrt 3 } \over 3}{a^3}\)
Vì CD // AB nên d(AB. CD) = d(AB, (SCD)). Hạ \(AH \bot SD\) , để ý rằng \(CD \bot (SAD) \Rightarrow AH \bot (SCD)\).
Do đó d(AB, SC) = AH.
Ta có: \(AH.SD = SA.AD\)
\(\Rightarrow AH = {{SA.AD} \over {\sqrt {S{A^2} + A{D^2}} }} = {{2a\sqrt 3 .a} \over {\sqrt {12{a^2} + {a^2}} }} = 2\sqrt {{3 \over {13}}} a\)
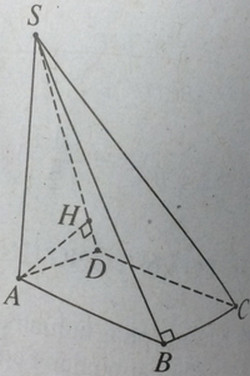
Bài 1.33: Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều cạnh bằng a. Gọi M, N và E theo thứ tự là trung điểm của BC, CC’ và C’A’. Đường thẳng EN cắt đường thẳng AC tại F, đường thẳng MN cắt đường thẳng B’C’ tại L. Đường thẳng FM kéo dài cắt AB tại I, đường thẳng LE kéo dài cắt A’B’ tại J.
Advertisements (Quảng cáo)
a) Chứng minh rằng các hình đa diện IBM.JB’L và A’EJ.AFI là những hình chóp cụt.
b) Tính thể tích khối chóp F.AIJA’
c) Chứng minh rằng mặt phẳng (MNE) chia khối lăng trụ đã cho thành hai khối đa diện có thể tích bằng nhau.
a) Gọi S là giao của hai đường thẳng MN và BB’. Khi đó S, I, J là điểm chung của cả hai mặt phẳng (MNE) và (ABB’A) nên chúng thẳng hàng. Do đó, ba đường thẳng BB’, MN và IJ đồng quy nên nó là một hình chóp cụt. Tương tự, đa diện A’EJ.AFI cũng là một hình chóp cụt.
b) Hai tam giác NCF và NC’E có \(\widehat C = \widehat {C’} = {90^0},NC = NC’,\widehat {CNF} = \widehat {C’NE}\) nên chúng bằng nhau.
Do đó, \(CF = C’E = {a \over 2}\)
Advertisements (Quảng cáo)
Tương tự, \(C’L = CM = {a \over 2}\) . Từ đó suy ra tam giác MCF cân ở C.
Ngoài ra ta còn có: \(\widehat {CMF} = \widehat {BMI} = {30^0}\) và \(\widehat {IBM} = {60^0}\) nên \(\widehat {MIB} = {90^0},IB = {{BM} \over 2} = {a \over 4}\) và \(IM = {{\sqrt 3 } \over 2}BM = {{\sqrt 3 } \over 4}a\)
Vì \(FI \bot AB,FI \bot {\rm{AA}}’\) nên \(FI \bot ({\rm{AIJ}}A’)\). Ta có diện tích hình thang vuông AA’JI bằng \({1 \over 2}({{3a} \over 4} + {a \over 4})b = {{ab} \over 2}\).
Gọi K là trung điểm của MF thì do tam giác MCF cân ở C nên \(CK \bot MF\) . Từ đó suy ra hai tam giác vuông CMK và BMI bằng nhau.
Do đó MF = MK = MI. Từ đó suy ra \(FI = {{3\sqrt 3 } \over 4}a\)
Vậy \({V_{F.{\rm{AIJ}}A’}} = {1 \over 3}({{ab} \over 2}){{3\sqrt 3 } \over 4}a = {{\sqrt 3 } \over 8}{a^2}b\)
c) Tương tự câu b) ta có \(C’L = CM = {a \over 2},LJ \bot A’B’\) và \(LJ = {{3\sqrt 3 } \over 4}a\).
Giả sử mặt phẳng (MNE) chia khối lăng trụ đã cho thành hai khối đa diện (H) và (H’) , trong đó (H’) là khối đa diện chứa đỉnh A, (H’) là khối đa diện chứa đỉnh B’.
Ta thấy \({V_{(H’)}} = {V_{IBM.JB’L}} – {V_{N.EC’L}},{V_{(H)}} = {V_{JA’E.{\rm{IAF}}}} – {V_{N.FCM}}\)
Vì \(\Delta IBM = \Delta JA’E,\Delta JB’L = \Delta {\rm{IAF,BB’ = AA}}’\) nên \({V_{IBM.JB’L}} = {V_{JA’E.{\rm{IAF}}}}\)
Ngoài ra hai hình chóp N.EC’L và N.FCM có đường cao bằng nhau và có đáy là những tam giác bằng nhau nên chúng có thể tích bằng nhau.
Từ đó suy ra V(H) = V(H’)
Bài 1.34: Cho hai đoạn thẳng AB và CD chéo nhau, AC là đường vuông góc chung của chúng. Biết rằng AC = h, AB = a, CD = b và góc giữa hai đường thẳng AB và CD bằng 600. Hãy tính thể tích của khối tứ diện ABCD.
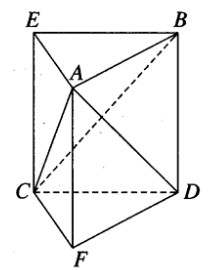
Dựng BE song song và bằng DC, DF song song và bằng BA. Khi đó, ABE.FDC là một lăng trụ đứng.
Ta có: \({S_{ABE}} = {1 \over 2}ab.\sin {60^0} = ab{{\sqrt 3 } \over 4}\) ,
\({V_{C.ABE}} = {1 \over 3}.{{\sqrt 3 } \over 4}ab.h = {{\sqrt 3 } \over {12}}abh\)
Từ đó suy ra \({V_{A.BCD}} = {V_{A.BCE}} = {{\sqrt 3 } \over {12}}abh\)

