Bài 1.35: Cho tứ diện đều ABCD. Gọi (H) là hình bát diện đều có các đỉnh là trung điểm các cạnh của tứ diện đều đó. Tính tỉ số \({{{V_{(H)}}} \over {{V_{ABCD}}}}\).

Gọi cạnh của tứ diện đều ABCD là a thì cạnh của hình bát diện đều (H) là \({a \over 2}\) . Khi đó \({V_{ABCD}} = {a^3}{{\sqrt 2 } \over {12}},{V_{(H)}} = {1 \over 3}{({a \over 2})^3}\sqrt 2 = {a^3}{{\sqrt 2 } \over {24}}\)
Từ đó suy ra \({{{V_{(H)}}} \over {{V_{ABCD}}}} = {1 \over 2}\).
Bài 1.36: Cho hình lập phương ABCD.A’B’C’D’ cạnh a, M là trung điểm của BB’. Tính theo a :
a) Khoảng cách giữa AC và DC’.
b) Độ dài đoạn vuông góc chung giữa CM và AB’.
Hướng dẫn làm bài
a) 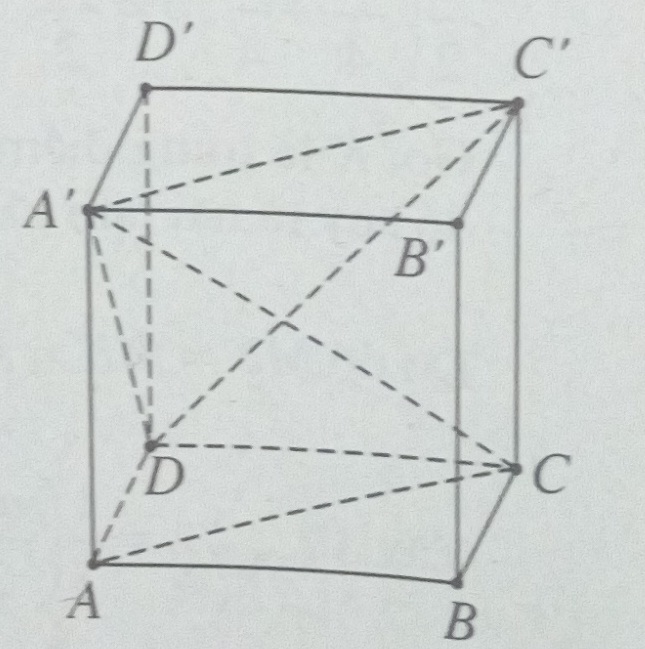
Gọi d(AC, DC’) = h
Ta có C’A’ // CA , do đó:
d(AC, DC’) = d(AC, (A’C’D)) = d(C, (A’C’D)) = h
Ta có: \({V_{A’.CDC’}} = {1 \over 3}{{{a^2}} \over 2}a = {{{a^3}} \over 6}\)
Để ý rằng tam giác A’C’D là tam giác đều cạnh bằng \(a\sqrt 2 \).
Do đó: \({S_{A’C’D}} = {{{a^2}\sqrt 3 } \over 2}\);
Advertisements (Quảng cáo)
\({V_{C.A’C’D}} = {1 \over 3}{S_{A’C’D}}.h = {1 \over 3}.{{{a^2}\sqrt 3 } \over 2}h = {V_{A’.CDC’}} = {{{a^3}} \over 6}\)
Từ đó suy ra: \(h = {{{{{a^3}} \over 6}} \over {{{{a^2}\sqrt 3 } \over 6}}} = {a \over {\sqrt 3 }} = {{a\sqrt 3 } \over 3}\)
b)

Từ A kẻ đường thẳng song song với MC’ , cắt DD’ tại N và A’D’ kéo dài tại J.
Đặt h1 = d(MC’ , AB’) = d(M, (AB’N))
Ta có: \({V_{M.AB’N}} = {V_{N.AB’M}} = {1 \over 3}{{{a^2}} \over 4}a = {{{a^3}} \over {12}}\)
Để ý rằng N là trung điểm của DD’ , A’J = 2A’D’ và JA = JB’
Gọi I là trung điểm của AB’, khi đó \(JI \bot AB’\).
Advertisements (Quảng cáo)
Ta có: \({\rm{AJ}} = \sqrt {{\rm{AA}}{‘^2} + A'{J^2}} = \sqrt {{a^2} + 4{a^2}} = a\sqrt 5 ;AI = {{a\sqrt 2 } \over 2}\)
Suy ra: \({\rm{IJ}} = \sqrt {5{a^2} – {{{a^2}} \over 2}} = {{3a} \over {\sqrt 2 }}\) ;
\({S_{JAB’}} = {1 \over 2}{{3a} \over {\sqrt 2 }}a\sqrt 2 = {{3{a^2}} \over 2}\)
Do đó: \({S_{AB’N}} = {1 \over 2}{S_{JAB’}} = {{3{a^2}} \over 4}\) ;
\({V_{M.AB’N}} = {1 \over 3}{{3{a^2}} \over 4}{h_1} = {{{a^2}{h_1}} \over 4} = {{{a^3}} \over {12}}\)
Suy ra: \({h_1} = {a \over 3}\)
Chú ý: Có thể tính thể tích SAB’N bằng cách khác.
Để ý rằng: \(NB’ = \sqrt {ND{‘^2} + B’D{‘^2}} = \sqrt {{{{a^2}} \over 4} + 2{a^2}} = {{3a} \over 2},\)
\(AN = {{a\sqrt 5 } \over 2},\,\,AB’ = a\sqrt 2 \)
Gọi \(\alpha = \widehat {NAB’}\) . Ta có: \(NB{^2} = {\rm{ }}A{N^2} + {\rm{ }}AB{^2}-{\rm{ }}2AN.AB.cos\alpha \)
Hay \({{9{a^2}} \over 4} = {{5{a^2}} \over 4} + 2{a^2} – 2{{a\sqrt 5 } \over 2}a\sqrt 2 \cos \alpha\)
\( \Rightarrow \cos \alpha = {1 \over {\sqrt {10} }} \Rightarrow \sin \alpha = {3 \over {\sqrt {10} }}\)
Do đó: \({S_{AB’N}} = {1 \over 2}AB’.AN.\sin \alpha = {1 \over 2}a\sqrt 2 {{a\sqrt 5 } \over 2}{3 \over {\sqrt {10} }} = {{3{a^2}} \over 4}\)
Bài 1.37: Cho tứ diện ABCD. Gọi hA , hB, hC, hD lần lượt là các đường cao của tứ diện xuất phát từ A, B, C, D và r là bán kính mặt cầu nội tiếp tứ diện. Chứng minh rằng:
\({1 \over {{h_A}}} + {1 \over {{h_B}}} + {1 \over {{h_C}}} + {1 \over {{h_D}}} = {1 \over r}\)


Gọi I là tâm mặt cầu nội tiếp tứ diện, V là thể tích tứ diện. Ta có
\(V = {V_{IBCD}} + {V_{ICDA}} + {V_{IDAB}} + {V_{IABC}}\)
\( \Rightarrow I = {{{V_{IBCD}}} \over V} + {{{V_{ICDA}}} \over V} + {{{V_{IDAB}}} \over V} + {{{V_{IABC}}} \over V}\)
\(= {{{1 \over 3}r{S_{BCD}}} \over {{1 \over 3}{h_A}{S_{BCD}}}} + {{{1 \over 3}r{S_{CDA}}} \over {{1 \over 3}{h_B}{S_{CDA}}}} + {{{1 \over 3}r{S_{DAB}}} \over {{1 \over 3}{h_C}{S_{DAB}}}} + {{{1 \over 3}r{S_{ABC}}} \over {{1 \over 3}{h_D}{S_{ABC}}}}\)
\( = r({1 \over {{h_A}}} + {1 \over {{h_B}}} + {1 \over {{h_C}}} + {1 \over {{h_D}}})\)
\(\Rightarrow {1 \over r} = {1 \over {{h_A}}} + {1 \over {{h_B}}} + {1 \over {{h_C}}} + {1 \over {{h_D}}}\)

