Bài 1.28: Hình được tạo thành từ hình lập phương ABCD.A’B’C’D’ khi ta bỏ đi các điểm trong của mặt phẳng (ABCD) có phải là một hình đa diện không?
Không phải là hình đa diện, vì trong hình đó có cạnh (chẳng hạn AB) không phải là cạnh chung của đúng hai đa giác.
Bài 1.29: Chứng minh rằng mỗi đỉnh của một hình đa diện là đỉnh chung của ít nhất ba cạnh.
Lấy một đỉnh B tùy ý của hình đa diện (H). Gọi M1 là một mặt của hình đa diện (H) chứa B. Gọi A, B, C là ba đỉnh liên tiếp của M1. Khi đó AB, BC là hai cạnh của (H). Gọi M2 là mặt khác với M1 và có chung cạnh AB với M1. Khi đó M2 còn có ít nhất một đỉnh D sao cho A, B, D là ba đỉnh khác nhau liên tiếp của M2. Nếu \(D \equiv C\) thì M1 và M2 có hai cạnh chung AB và BC, điều này vô lí. Vậy D phải khác C. Do đó qua đỉnh B có ít nhất ba cạnh BA, BC và BD.
Advertisements (Quảng cáo)
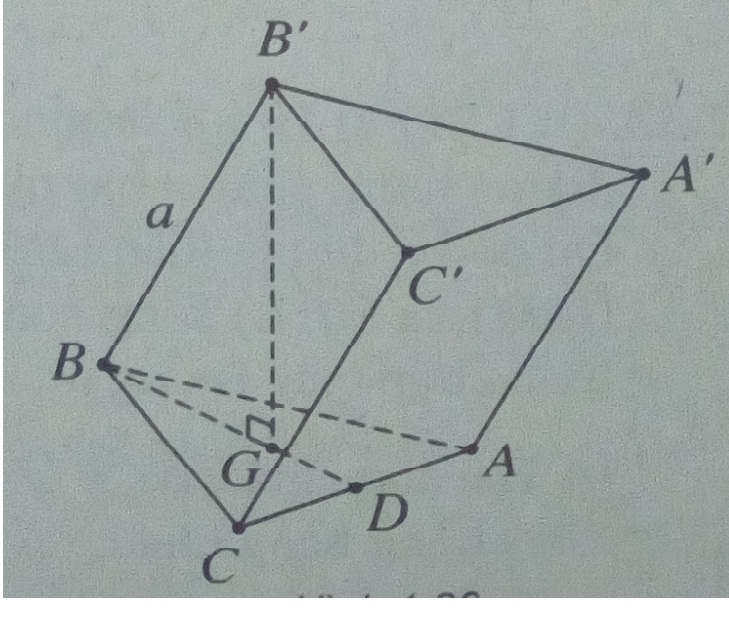
Bài 1.30: Cho hình lăng trị ABC.A’B’C’ có đáy là tam giác vuông cân ở C. Cạnh B’B = a và tạo với đáy một góc bằng 600. Hình chiếu vuông góc hạ từ B’ lên đáy trùng với trọng tâm của tam giác ABC. Tính thể tích khối lăng trụ đó theo a.
Advertisements (Quảng cáo)
Gọi G là trọng tâm của tam giác ABC, khi đó \(\widehat {B’BG} = {60^0},B’G = {{a\sqrt 3 } \over 2},BG = {a \over 2}\)
Gọi D là trung điểm của AC, khi đó \(BD = {{3a} \over 4}\) .
Ta có BC2 + CD2 = BD2 , do đó \(B{C^2} + {{B{C^2}} \over 4} = {{5B{C^2}} \over 4} = {{9{a^2}} \over {16}}\)
Suy ra \(B{C^2} = {9 \over {20}}{a^2},{S_{ABC}} = {{B{C^2}} \over 2} = {9 \over {40}}{a^2}\)
\({V_{ABC.A’B’C’}} = {{a\sqrt 3 } \over 2}.{{9{a^2}} \over {40}} = {{9\sqrt 3 } \over {80}}{a^3}\)
Bài 1.31: Tính thể tích khối lăng trụ có chiều cao bằng h, đáy là ngũ giác đều nội tiếp trong một đường tròn bán kính r.
Chia đáy của hình lăng trụ đã cho thành năm tam giác cân có chung đỉnh O là tâm đường tròn ngoại tiếp đáy. Khi đó diện tích đáy bằng \({5 \over 2}{r^2}\sin {72^0}\) . Do đó thể tích lăng trụ đó bằng \({5 \over 2}h{r^2}\sin {72^0}\).

