Câu 1: Biểu diễn dao động điều hòa có phương trình: x = Acos(ωt + Ø) (*)
Các bước:
+ Vẽ trục tọa độ Ox nằm ngang
+ Vẽ vecto OM 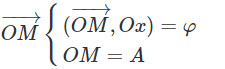
+ Khi t = 0 ,cho vecto OM quay đều quanh O với tốc độ góc ω.
Khi đó, vecto quay OM biểu diễn dao động điều hòa có phương trình (*)
Câu 2: Phương pháp giản đồ Fre-nen: Lần lượt vẽ hai vecto quay biểu diễn hai phương trình dao động thành phần. Sau đó vẽ tổng hai vecto trên. Vecto tổng là vecto quay biểu diễn phương trình của dao động tổng hợp.
Câu 3: a) Hai dao động thành phần cùng pha: biên độ dao động tổng hợp là lớn nhất và bằng tổng hai biên độ: A = A1 + A2
b) Hai dao động thành phần ngược pha: biên độ dao động tổng hợp là nhỏ nhất và bằng giá trị tuyệt đối của hiệu hai biên độ: A = |A1 – A2|
c) Hai dao động có thành phần có pha vuông góc: A = √ (A12 + A22)
Bài 4: Chọn đáp án đúng.
Hai dao động là ngược chiều khi:
A. φ2 – φ1 = 2nπ.
Advertisements (Quảng cáo)
B. φ2 – φ1 = nπ.
C. φ2 – φ1 = (n – 1)π.
D. φ2 – φ1 = (2n – 1)π.
 D.
D.
Bài 5: Xét một vectơ quay \(\overrightarrow{OM}\) có những đặc điểm sau:
– Có độ lớn bằng hai dơn vị chiều dài.
Advertisements (Quảng cáo)
– Quay quanh O với tốc độ góc 1 rad/s.
– Tại thời điểm t = 0, vectơ \(\overrightarrow{OM}\) hợp với trục Ox một góc 300.
Hỏi vec tơ quay \(\overrightarrow{OM}\) biểu diễn phương trình của dao động điều hòa nào?
A. x = 2cos(t – \(\frac{\pi }{3}\)).
B. x = 2cos(t + \(\frac{\pi }{6}\)).
C. x = 2cos(t – 300).
D. x = 2cos(t + \(\frac{\pi }{3}\)).
B. Phương trình tổng quát: x = Acos(ωt + φ).
+ Biên độ: A = 2 đơn vị chiều dài.
+ Tần số góc: ω = 1rad/s.
+ Pha ban đầu: φ = 300 = \(\frac{\pi }{6}\).
Bài 6: Cho hai dao động điều hòa cùng phương, cùng tần số góc ω = 5π rad/s, với các biên độ:
A1 = \(\frac{\sqrt{3}}{2}\) cm, A2 = √3 cm và các pha ban đầu tương ứng φ1 = \(\frac{\pi }{2}\) và φ2 = \(\frac{5\pi }{6}.\)
Tìm phương trìn dao động tổng hợp của hai dao động trên.
Áp dụng công thức (5.1 và 5.2 – SGK) ta tìm được:
A = 2,3 cm và φ = 0,73π
Phương trình dao động tổng hợp là: x = 2,3cos(5πt + 0,73π) (cm).

